【题目】某区共有甲、乙、丙三所高中,所有高二学生参加了一次数学测试.老师们对其中的一道题进行了分析,把每个学生的解答情况归结为下列四类情况之一:A﹣﹣概念错误;B﹣﹣计算错误;C﹣﹣解答基本正确,但不完整;D﹣﹣解答完全正确.各校出现这四类情况的人数分别占本校高二学生数的百分比如下表所示.
A | B | C | D | |
甲校(%) | 2.75 | 16.25 | 60.75 | 20.25 |
乙校(%) | 3.75 | 22.50 | 41.25 | 32.50 |
丙校(%) | 12.50 | 6.25 | 22.50 | 58.75 |
已知甲校高二有400名学生,这三所学校高二学生人数的扇形统计图如图.
根据以上信息,解答下列问题:
(1)求全区高二学生总数;
(2)求全区解答完全正确的学生数占全区高二学生总数的百分比m(精确到0.01%);
(3)请你对表中三校的数据进行对比分析,给丙校高二数学老师提一个值得关注的问题,并说明理由. 
参考答案:
【答案】
(1)解:全区高二学生总数=400÷ ![]() =1200人
=1200人
(2)解:乙校人数=1200× ![]() =480人,丙校人数=1200×
=480人,丙校人数=1200× ![]() =320人,
=320人,
∴D总人数=400×20.25%+480×32.50%+320×58.75%=425,
∴全区解答完全正确的学生数占全区高二学生总数的百分比m= ![]() =35.42%
=35.42%
(3)解:丙校的学生犯概念性的错误所占的比例很大,丙校的老师应加强概念的理解及掌握
【解析】(1)根据甲校得人数及在扇形中所占的比例即可得出全区高二学生总数.(2)根据(1)的结果可求出全区解答完全正确的学生数,进而可得出全区解答完全正确的学生数占全区高二学生总数的百分比m.(3)根据概念错误所占的比例可提一些这方面的建议.
【考点精析】本题主要考查了统计表和扇形统计图的相关知识点,需要掌握制作统计表的步骤:(1)收集整理数据.(2)确定统计表的格式和栏目数量,根据纸张大小制成表格.(3)填写栏目、各项目名称及数据.(4)计算总计和合计并填入表中,一般总计放在横栏最左格,合计放在竖栏最上格.(5)写好表格名称并标明制表时间;能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.
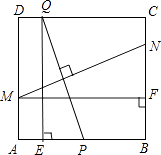
(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AB=1,BC=
 ,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.
,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E. 
(1)求AE的长度;
(2)分别以点A、E为圆心,AB长为半径画弧,两弧交于点F(F与C在AB两侧),连接AF、EF,设EF交弧DE所在的圆于点G,连接AG,试猜想∠EAG的大小,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1) ;
;
(2)a(a﹣3)+(2﹣a)(2+a). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架飞机由A向B沿水平直线方向飞行,在航线AB的正下方有两个山头C、D.飞机在A处时,测得山头C、D在飞机的前方,俯角分别为60°和30°.飞机飞行了6千米到B处时,往后测得山头C的俯角为30°,而山头D恰好在飞机的正下方.求山头C、D之间的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】张经理到老王的果园里一次性采购一种水果,他俩商定:张经理的采购价y(元/吨)与采购量x(吨)之间函数关系的图象如图中的折线段ABC所示(不包含端点A,但包含端点C).

(1)求y与x之间的函数关系式;
(2)已知老王种植水果的成本是2 800元/吨,那么张经理的采购量为多少时,老王在这次买卖中所获的利润w最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动.
(1)请在所给的图中,用尺规画出点A在正方形整个翻滚过程中所经过的路线图;
(2)求正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S.
相关试题

