Question

【题目】如图，在边长为2的正方形ABCD中，P为AB的中点，Q为边CD上一动点，设DQ=t（0≤t≤2），线段PQ的垂直平分线分别交边AD、BC于点M、N，过Q作QE⊥AB于点E，过M作MF⊥BC于点F．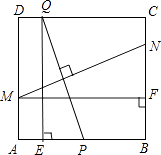
（1）当t≠1时，求证：△PEQ≌△NFM；
（2）顺次连接P、M、Q、N，设四边形PMQN的面积为S，求出S与自变量t之间的函数关系式，并求S的最小值．

Answer 1

【答案】
（1）证明：∵四边形ABCD是正方形，

∴∠A=∠B=∠D=90°，AD=AB，

∵QE⊥AB，MF⊥BC，

∴∠AEQ=∠MFB=90°，

∴四边形ABFM、AEQD都是矩形，

∴MF=AB，QE=AD，MF⊥QE，

又∵PQ⊥MN，

∴∠1+∠EQP=90°，∠2+∠FMN=90°，

∵∠1=∠2，

∴∠EQP=∠FMN，

又∵∠QEP=∠MFN=90°，

∴△PEQ≌△NFM

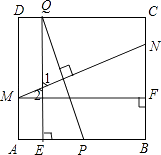
（2）解：分为两种情况：①当E在AP上时，

∵点P是边AB的中点，AB=2，DQ=AE=t，

∴PA=1，PE=1﹣t，QE=2，

由勾股定理，得PQ= = ，

∵△PEQ≌△NFM，

∴MN=PQ= ，

又∵PQ⊥MN，

∴S= = = t2﹣t+ ，

∵0≤t≤2，

∴当t=1时，S最小值=2．

②当E在BP上时，

∵点P是边AB的中点，AB=2，DQ=AE=t，

∴PA=1，PE=t﹣1，QE=2，

由勾股定理，得PQ= = ，

∵△PEQ≌△NFM，

∴MN=PQ= ，

又∵PQ⊥MN，

∴S= = [（t﹣1）2+4]= t2﹣t+ ，

∵0≤t≤2，

∴当t=1时，S最小值=2．

综上：S= t2﹣t+ ，S的最小值为2．

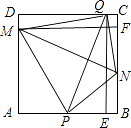
【解析】（1）由四边形ABCD是正方形得到∠A=∠B=∠D=90°，AD=AB，又由∠EQP=∠FMN，而证得；（2）分为两种情况：①当E在AP上时，由点P是边AB的中点，AB=2，DQ=AE=t，又由勾股定理求得PQ，由△PEQ≌△NFM得到PQ的值，又PQ⊥MN求得面积S，由t范围得到S的最小值；②当E在BP上时，同法可求S的最小值．