【题目】某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情况,随机调查了若干名学生,根据调查数据进行整理,绘制了如下的不完整统计图.
请你根据以上的信息,回答下列问题:
(1)本次共调查了名学生,其中最喜爱戏曲的有人;在扇形统计图中,最喜爱体育的对应扇形的圆心角大小是 .
(2)根据以上统计分析,估计该校2000名学生中最喜爱新闻的人数.
参考答案:
【答案】
(1)50,3,72°
(2)解:2000×8%=160(人),
答:估计该校2000名学生中最喜爱新闻的人数约有160人.
【解析】解:(1)本次共调查学生:4÷8%=50(人),最喜爱戏曲的人数为:50×6%=3(人);
∵“娱乐”类人数占被调查人数的百分比为: ![]() ×100%=36%,
×100%=36%,
∴“体育”类人数占被调查人数的百分比为:1﹣8%﹣30%﹣36%﹣6%=20%,
∴在扇形统计图中,最喜爱体育的对应扇形的圆心角大小是360°×20%=72°;
(2)2000×8%=160(人),
答:估计该校2000名学生中最喜爱新闻的人数约有160人.
故答案为:(1)50,3,72°;(2)160.
(1)由条形统计图可得到喜欢新闻的频数,由扇形统计图可得到喜欢新闻的百分比,然后依据总人数=频数÷百分比求解即可,依据频数=总数×百分比可求得喜欢戏曲的人数,最后依据圆心角=360°×百分比求解即可;
(2)用全校的人数×喜欢新闻人数的百分比即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具厂要生产500个芭比娃娃,此生产任务由甲、乙、丙三台机器承担,甲机器每小时生产12个,乙、丙两台机器的每小时生产个数之比为4:5.若甲、乙、丙三台机器同时生产,刚好在10小时25分钟完成任务.
(1)求乙、丙两台机器每小时各生产多少个?
(2)由于某种原因,三台机器只能按一定次序循环交替生产,且每台机器在每个循环中只能生产1小时,即每个循环需要3小时.
①若生产次序为甲、乙、丙,则最后一个芭比娃娃由 机器生产完成,整个生产过程共需 小时;
②若想使完成生产任务的时间最少,直接写出三台机器的生产次序及完成生产任务的最少时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为
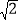 ;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )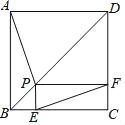
A. ①②③B. ①②④C. ②③④D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).

(1)求反比例函数的解析式;
(2)反比例函数的图象与线段BC交于点D,直线
 过点D,与线段AB相交于点F,求点F的坐标;
过点D,与线段AB相交于点F,求点F的坐标;(3)连接OF,OE,探究∠AOF与∠EOC的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上表示的数如图所示,动点P从点A出发,沿数轴向右以每秒1个单位长度的速度向点B运动到点B停止运动;同时,动点Q从点B出发,沿数轴向左以每秒2个单位长度的速度向点A运动,到点A停止运动设点P运动的时间为t秒,P、Q两点的距离为d(d≥0)个单位长度.
(1)当t=1时,d= ;
(2)当P、Q两点中有一个点恰好运动到线段AB的中点时,求d的值;
(3)当点P运动到线段AB的3等分点时,直接写出d的值;
(4)当d=5时,直接写出t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为加强中小学生体育运动,某市第十七届中小学生田径运动会在市体育场举行,体育场主席台侧面如图所示,若顶棚顶端D与看台底端A的连线和地面垂直,测得顶棚CD的长为12米,∠BAC=30°,∠ACD=45°,求看台AC的长.(结果保留一位小数,参考数据:
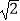 ≈1.41,
≈1.41, 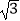 ≈1.73)
≈1.73)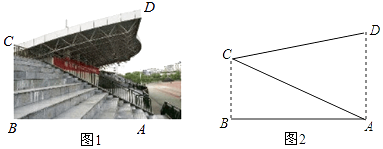
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
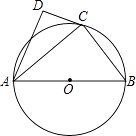
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
相关试题

