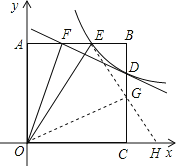
【题目】如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).

(1)求反比例函数的解析式;
(2)反比例函数的图象与线段BC交于点D,直线![]() 过点D,与线段AB相交于点F,求点F的坐标;
过点D,与线段AB相交于点F,求点F的坐标;
(3)连接OF,OE,探究∠AOF与∠EOC的数量关系,并证明.
参考答案:
【答案】(1)y=![]() ;(2)(2,4).(3)∠AOF=
;(2)(2,4).(3)∠AOF=![]() ∠EOC.见解析
∠EOC.见解析
【解析】
试题分析:(1)设反比例函数的解析式为y=![]() ,把点E(3,4)代入即可求出k的值,进而得出结论;
,把点E(3,4)代入即可求出k的值,进而得出结论;
(2)由正方形AOCB的边长为4,故可知点D的横坐标为4,点F的纵坐标为4.由于点D在反比例函数的图象上,所以点D的纵坐标为3,即D(4,3),由点D在直线y=﹣![]() x+b上可得出b的值,进而得出该直线的解析式,再把y=4代入直线的解析式即可求出点F的坐标;
x+b上可得出b的值,进而得出该直线的解析式,再把y=4代入直线的解析式即可求出点F的坐标;
(3)在CD上取CG=AF=2,连接OG,连接EG并延长交x轴于点H,由全等三角形的判定定理可知△OAF≌△OCG,△EGB≌△HGC(ASA),故可得出EG=HG.设直线EG的解析式为y=mx+n,把E(3,4),G(4,2)代入即可求出直线EG的解析式,故可得出H点的坐标,在Rt△AOF中,AO=4,AE=3,根据勾股定理得OE=5,可知OH=OE,即OG是等腰三角形底边EF上的中线.所以OG是等腰三角形顶角的平分线,由此即可得出结论.
解:(1)设反比例函数的解析式y=![]() ,
,
∵反比例函数的图象过点E(3,4),
∴4=![]() ,即k=12.
,即k=12.
∴反比例函数的解析式y=![]() ;
;
(2)∵正方形AOCB的边长为4,
∴点D的横坐标为4,点F的纵坐标为4.
∵点D在反比例函数的图象上,
∴点D的纵坐标为3,即D(4,3).
∵点D在直线y=﹣![]() x+b上,
x+b上,
∴3=﹣![]() ×4+b,解得b=5.
×4+b,解得b=5.
∴直线DF为y=﹣![]() x+5,
x+5,
将y=4代入y=﹣![]() x+5,得4=﹣
x+5,得4=﹣![]() x+5,解得x=2.
x+5,解得x=2.
∴点F的坐标为(2,4).
(3)∠AOF=![]() ∠EOC.
∠EOC.
证明:在CD上取CG=AF=2,连接OG,连接EG并延长交x轴于点H.
∵AO=CO=4,∠OAF=∠OCG=90°,AF=CG=2,
∴△OAF≌△OCG(SAS).
∴∠AOF=∠COG.
∵∠EGB=∠HGC,∠B=∠GCH=90°,BG=CG=2,
∴△EGB≌△HGC(ASA).
∴EG=HG.
设直线EG:y=mx+n,
∵E(3,4),G(4,2),
∴![]() ,解得,
,解得,![]() .
.
∴直线EG:y=﹣2x+10.
令y=﹣2x+10=0,得x=5.
∴H(5,0),OH=5.
在Rt△AOE中,AO=4,AE=3,根据勾股定理得OE=5.
∴OH=OE.
∴OG是等腰三角形底边EH上的中线.
∴OG是等腰三角形顶角的平分线.
∴∠EOG=∠GOH.
∴∠EOG=∠GOC=∠AOF,即∠AOF=![]() ∠EOC.
∠EOC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在用描点法画二次函数y=ax2+bx+c图象时,由于粗心,他算错了一个y值,列出了下面表格:
x
…
﹣1
0
1
2
3
…
y=ax2+bx+c
…
5
3
2
3
6
…
(1)请指出这个错误的y值,并说明理由;
(2)若点M(a,y1),N(a+4,y2)在二次函数y=ax2+bx+c图象上,且a>﹣1,试比较y1与y2的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a3+a4=a7 B.a3a4=a7 C.(a3)4=a7 D.a6÷a3=a2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC与△A′B′C′中,有下列条件:(1)
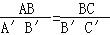 ;(2)
;(2)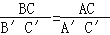 ;(3)∠A=∠A′;(4)∠C=∠C′.如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有多少组( )
;(3)∠A=∠A′;(4)∠C=∠C′.如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有多少组( )A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a2+a3=a5 B.a2a3=a6
C.(a2)3=a5 D.a5÷a2=a3
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中是确定事件的为( )
A. 两条线段可以组成一个三角形 B. 打开电视机正在播放动画片
C. 车辆随机经过一个路口,遇到绿灯 D. 掷一枚均匀的骰子,掷出的点数是奇数
相关试题

