【题目】某校开展“爱我海珠,创卫同行”的活动,倡议学生利用双休日在海珠湿地公园参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息解答下列问题:
(1)将条形统计图补充完整.
(2)抽查的学生劳动时间的众数为 , 中位数为 .
(3)已知全校学生人数为1200人,请你估算该校学生参加义务劳动1小时的有多少人?
参考答案:
【答案】
(1)解:如图所示:

(2)1.5,1.5
(3)解:1200×30%=400,
答:估算该校学生参加义务劳动1小时的有400人.
【解析】解:(1)根据题意得:30÷30%=100(人),
∴学生劳动时间为“1.5小时”的人数为100﹣(12+30+18)=40(人),
补全统计图,如图所示:

⑵根据题意得:抽查的学生劳动时间的众数为1.5小时、中位数为1.5小时,
所以答案是:1.5、1.5;
【考点精析】掌握条形统计图和中位数、众数是解答本题的根本,需要知道能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况;中位数是唯一的,仅与数据的排列位置有关,它不能充分利用所有数据;众数可能一个,也可能多个,它一定是这组数据中的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设置了两种促销方式.一种方式是:让顾客通过转转盘获得购物券.规定顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准100元、50元、20元的相应区域,那么顾客就可以分别获得100元、50元、20元购物券,凭购物券可以在该商场继续购物;如果指针对准其他区域,那么就不能获得购物券.另一种方式是:不转转盘,顾客每购买100元的商品,可直接获得10元购物券.据统计,一天中共有1 000人次选择了转转盘的方式,其中指针落在100元、50元、20元的次数分别为50次、100次、200次.
(1)指针落在不获奖区域的概率约是多少?
(2)通过计算说明选择哪种方式更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数m,n满足m﹣n2=1,则代数式m2+2n2+4m﹣1的最小值等于______.
-
科目: 来源: 题型:
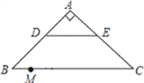
查看答案和解析>>【题目】如图,在Rt△ABC中.∠A=90°.AB=AC,BC=20,DE是△ABC的中位线.点M是边BC上一点.BM=3.点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:y1=x+m与直线l2:y2=nx+3相交于点C(1,2).
(1)求m、n的值.
(2)在给出的直角坐标系中画出直线l1和直线l2的图象.
(3)求nx+3>x+m的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N. 给出下列结论:①△ABM≌△CDN;②AM=
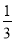 AC;③DN=2NF;④S△AMB=
AC;③DN=2NF;④S△AMB=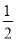 S△ABC.其中正确的结论是_______________(只填番号)
S△ABC.其中正确的结论是_______________(只填番号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE是△ABC的中位线,过点C作CF∥BD交DE的延长线于点F.
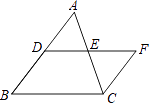
(1)求证:DE=EF.
(2)分别连结DC、AF,若AC=BC,试判断四边形ADCF的形状,并说明理由.
相关试题

