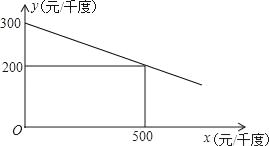
【题目】某工厂在生产过程中要消耗大量电能,消耗每千度电产生利润与电价是一次函数关系,经过测算,工厂每千度电产生利润y(元/千度))与电价x(元/千度)的函数图象如图:
(1)请求出y与x之间的函数关系式;
(2)为了实现节能减排目标,有关部门规定,该厂电价x(元/千度)与每天用电量m(千度)的函数关系为x=20m+500,且该工厂每天用电量不超过50千度,为了获得最大利润w,工厂每天应安排使用多少度电?工厂每天消耗电产生利润最大是多少元?
参考答案:
【答案】(1)y=﹣0.2x+300(x≥0);(2)当工厂每天消耗50千度电时,工厂每天消耗电产生利润为最大,最大利润为1875元.
【解析】试题分析:(1)利用待定系数法可以求得工厂每千度电产生利润y与电价x的函数解析式;
(2)设工厂每天消耗电产生利润为W元,根据关系式“每天消耗电产生利润=每天用电量×每千度电产生的利润”便可得到W与m的函数关系式;
利用配方法对上述表达式进行配方,结合二次函数性质即可求得W的最大值.
解:(1)设工厂每千度电产生利润y(元/千度)与电价x(元/千度)的函数解析式为:y=kx+b,
∵该函数图象过点(0,300),(500,200),
∴![]() ,
,
解得![]() .
.
所以y=﹣0.2x+300(x≥0),
(2)设工厂每天消耗电产生利润为w元,由题意得:
w=my=m(﹣0.2x+300)
=m[﹣0.2(20m+500)+300]
=﹣4m2+200m
=﹣4(m﹣25)2+2500,
在m≤25时,w随m的增大而最大,
由题意,m≤50,
∴当m=50时,w最大=﹣(50﹣25)2+2500=1875,
即当工厂每天消耗50千度电时,工厂每天消耗电产生利润为最大,最大利润为1875元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂按用户的月需求量x(件)完成一种产品的生产,其中x>0.每件的售价为18万元,每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比.经市场调研发现,月需求量x与月份n(n为整数,1≤n≤12)符合关系式x=2n2﹣2kn+9(k+3)(k为常数),且得到了表中的数据
月份n(月)1
1
2
成本y(万元/件)
11
12
需求量x(件/月)
120
100
(1)直接写出k的值;
(2)求y与x满足的关系式,请说明一件产品的利润能否是12万元;
(3)推断是否存在某个月既无盈利也不亏损.
-
科目: 来源: 题型:
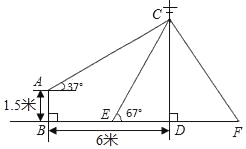
查看答案和解析>>【题目】如图,在电线杆CD处引拉线CE,CF固定电线杆,拉线CE和地面所成的角∠CED=67°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为37°,求拉线CE的长(参考数据:sin67°≈
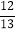 ,cos67°≈
,cos67°≈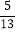 ,tan67°≈
,tan67°≈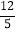 ,sin37°≈
,sin37°≈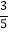 ,cos37°≈
,cos37°≈ ,tsn37°≈
,tsn37°≈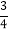 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E,F分别在边AB,BC上,∠ADE=∠CDF.
(1)求证:AE=CF;
(2)连接DB交EF于点O,延长OB至G,使OG=OD,连接EG,FG,判断四边形DEGF是否是菱形,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分6分)某公司调查某中学学生对其环保产品的了解情况,随机抽取该校部分学生进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为A、B、C、D.根据调查结果绘制了如下尚不完整的统计图.

(1)本次问卷共随机调查了 名学生,扇形统计图中m= .
(2)请根据数据信息补全条形统计图;
(3)若该校有1000名学生,估计选择“非常了解”、“比较了解”共约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
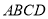 的对角线
的对角线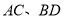 交于点
交于点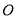 ,直角三角形
,直角三角形 绕点
绕点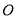 按逆时针旋转,
按逆时针旋转,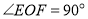
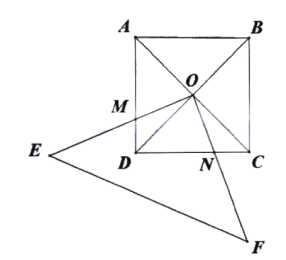
(1)若直角三角形绕点
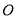 逆时针转动过程中分别交
逆时针转动过程中分别交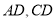 两边于
两边于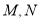 两点
两点①求证:
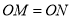 ;
;②连接
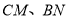 ,那么
,那么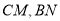 有什么样的关系?试说明理由
有什么样的关系?试说明理由(2)若正方形的边长为2,则正方形
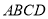 与
与 两个图形重叠部分的面积为多少?(不需写过程直接写出结果)
两个图形重叠部分的面积为多少?(不需写过程直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.

相关试题

