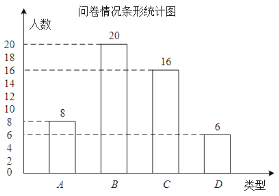
【题目】(本题满分6分)某公司调查某中学学生对其环保产品的了解情况,随机抽取该校部分学生进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为A、B、C、D.根据调查结果绘制了如下尚不完整的统计图. 
(1)本次问卷共随机调查了 名学生,扇形统计图中m= .
(2)请根据数据信息补全条形统计图;
(3)若该校有1000名学生,估计选择“非常了解”、“比较了解”共约有多少人?
参考答案:
【答案】(1)50; 32;(2)见解析;(3)560人.
【解析】(1)由条形统计图和扇形统计图可知,用“非常了解”的人数为8人除以所占比例为16%,即可求得总人数;“一般了解”的人数为16人除以总人数即可求所占比例;
(2)用总人数减去B、C、D部分的人数求出A部分的人数,然后补全条形统计图即可;
(3)先根据扇形统计图得到部分学生“非常了解”和“比较了解”的人数占样本总人数的比例,再由样本估计总体即可求解.
(1)8÷16%=50人;
16÷50=32%.
(2)50-20-16-6=8人.如图,
(3)1000×(16%+40%)=560人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2.若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,下图①为点P,Q的“相关矩形”的示意图.
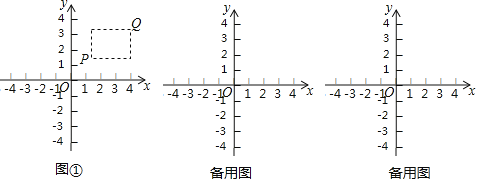
已知点A的坐标为(1,0),
(1)若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
(2)点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(3)若点D的坐标为(4,2),将直线y=2x+b平移,当它与点A,D的“相关矩形”没有公共点时,求出b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
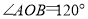 (本题中的角均大于
(本题中的角均大于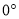 且小于
且小于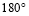 )
)(1)如图1,在
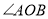 内部作
内部作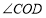 ,若
,若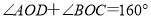 ,求
,求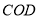 的度数;
的度数;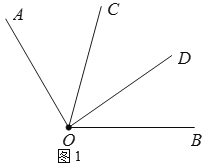
(2)如图2,在
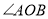 内部作
内部作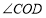 ,
,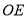 在
在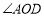 内,
内,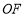 在
在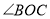 内,且
内,且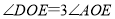 ,
,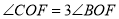 ,
,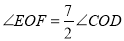 ,求
,求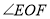 的度数;
的度数;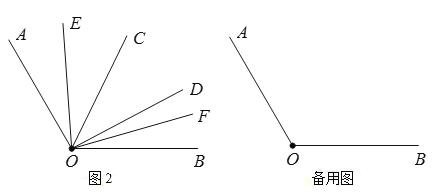
(3)射线
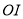 从
从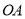 的位置出发绕点
的位置出发绕点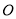 顺时针以每秒
顺时针以每秒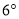 的速度旋转,时间为
的速度旋转,时间为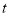 秒(
秒(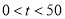 且
且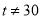 ).射线
).射线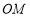 平分
平分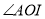 ,射线
,射线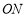 平分
平分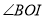 ,射线
,射线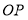 平分
平分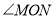 .若
.若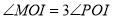 ,则
,则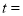 秒.
秒. -
科目: 来源: 题型:
查看答案和解析>>【题目】学习概率知识后,小庆和小丽设计了一个游戏,在一个不透明的布袋A里面装有三个分别标有数字3,4,5的小球(小球除数字不同外,其余都相同);同时制作了一个可以自由转动的转盘B,转盘B被平均分成2部分,在每一部分内分别标上数字1,2.现在其中一人从布袋A中随机摸取一个小球,记下数字为x;另一人转动转盘B,转盘停止后,指针指向的数字记为y(若指针指在边界线上时视为无效,重新转动),从而确定点P的坐标为P(x,y).
(1)请用树状图或列表的方法写出所有可能得到的点P的坐标;
(2)若S=xy,当S为奇数时小庆获胜,否则小丽获胜,你认为这个游戏公平吗?对谁更有利呢?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
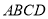 的对角线
的对角线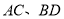 交于点
交于点 ,直角三角形
,直角三角形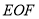 绕点
绕点 按逆时针旋转,
按逆时针旋转,
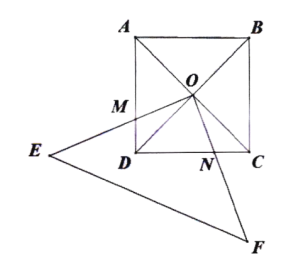
(1)若直角三角形绕点
 逆时针转动过程中分别交
逆时针转动过程中分别交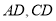 两边于
两边于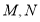 两点
两点①求证:
 ;
;②连接
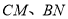 ,那么
,那么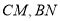 有什么样的关系?试说明理由
有什么样的关系?试说明理由(2)若正方形的边长为2,则正方形
 与
与 两个图形重叠部分的面积为多少?(不需写过程直接写出结果)
两个图形重叠部分的面积为多少?(不需写过程直接写出结果) -
科目: 来源: 题型:
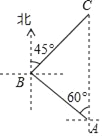
查看答案和解析>>【题目】科技改变生活,手机导航极大方便了人们的出行,如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶12千米至B地,再沿北偏东45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,求B,C两地的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 两点分别是
两点分别是 轴和
轴和 轴正半轴上两个动点,以三点
轴正半轴上两个动点,以三点 为顶点的矩形
为顶点的矩形 的面积为24,反比例函数
的面积为24,反比例函数 (
( 为常数且
为常数且 )的图象与矩形
)的图象与矩形 的两边
的两边 分别交于点
分别交于点 .
.
(1)若
 且点
且点 的横坐标为3.
的横坐标为3.①点
 的坐标为 ,点
的坐标为 ,点 的坐标为 (不需写过程,直接写出结果);
的坐标为 (不需写过程,直接写出结果);②在
 轴上是否存在点
轴上是否存在点 ,使
,使 的周长最小?若存在,请求出
的周长最小?若存在,请求出 的周长最小值;若不存在,请说明理由.
的周长最小值;若不存在,请说明理由.(2)连接
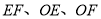 ,在点
,在点 的运动过程中,
的运动过程中, 的面积会发生变化吗?若变化,请说明理由,若不变,请用含
的面积会发生变化吗?若变化,请说明理由,若不变,请用含 的代数式表示出
的代数式表示出 的面积.
的面积.
相关试题

