【题目】如图,在电线杆CD处引拉线CE,CF固定电线杆,拉线CE和地面所成的角∠CED=67°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为37°,求拉线CE的长(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,sin37°≈
,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tsn37°≈
,tsn37°≈![]() ).
).
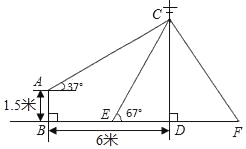
参考答案:
【答案】拉线CE的长约为6.5米.
【解析】试题分析:题意可先过点A作AH⊥CD于H.在Rt△ACH中,可求出CH,进而CD=CH+HD=CH+AB,再在Rt△CED中,求出CE的长.
解:过点A作AH⊥CD,垂足为H,
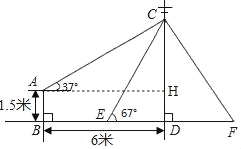
由题意可知四边形ABDH为矩形,∠CAH=37°,
∴AB=DH=1.5,BD=AH=6,
在Rt△ACH中,tan∠CAH=![]() ,
,
∴CH=AHtan∠CAH,
∴CH=AHtan∠CAH=6tan37°=6×![]() =
=![]() (米),
(米),
∵DH=1.5,
∴CD=![]() +1.5=6,
+1.5=6,
在Rt△CDE中,
∵∠CED=67°,sin∠CED=![]() ,
,
∴CE=![]() =
=![]() (米),
(米),
答:拉线CE的长约为![]() 米.
米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】科技改变生活,手机导航极大方便了人们的出行,如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶12千米至B地,再沿北偏东45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,求B,C两地的距离.
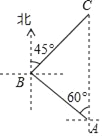
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 两点分别是
两点分别是 轴和
轴和 轴正半轴上两个动点,以三点
轴正半轴上两个动点,以三点 为顶点的矩形
为顶点的矩形 的面积为24,反比例函数
的面积为24,反比例函数 (
( 为常数且
为常数且 )的图象与矩形
)的图象与矩形 的两边
的两边 分别交于点
分别交于点 .
.
(1)若
 且点
且点 的横坐标为3.
的横坐标为3.①点
 的坐标为 ,点
的坐标为 ,点 的坐标为 (不需写过程,直接写出结果);
的坐标为 (不需写过程,直接写出结果);②在
 轴上是否存在点
轴上是否存在点 ,使
,使 的周长最小?若存在,请求出
的周长最小?若存在,请求出 的周长最小值;若不存在,请说明理由.
的周长最小值;若不存在,请说明理由.(2)连接
 ,在点
,在点 的运动过程中,
的运动过程中, 的面积会发生变化吗?若变化,请说明理由,若不变,请用含
的面积会发生变化吗?若变化,请说明理由,若不变,请用含 的代数式表示出
的代数式表示出 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂按用户的月需求量x(件)完成一种产品的生产,其中x>0.每件的售价为18万元,每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比.经市场调研发现,月需求量x与月份n(n为整数,1≤n≤12)符合关系式x=2n2﹣2kn+9(k+3)(k为常数),且得到了表中的数据
月份n(月)1
1
2
成本y(万元/件)
11
12
需求量x(件/月)
120
100
(1)直接写出k的值;
(2)求y与x满足的关系式,请说明一件产品的利润能否是12万元;
(3)推断是否存在某个月既无盈利也不亏损.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E,F分别在边AB,BC上,∠ADE=∠CDF.
(1)求证:AE=CF;
(2)连接DB交EF于点O,延长OB至G,使OG=OD,连接EG,FG,判断四边形DEGF是否是菱形,并说明理由.

-
科目: 来源: 题型:
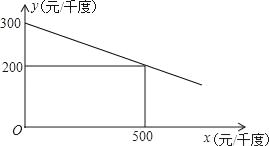
查看答案和解析>>【题目】某工厂在生产过程中要消耗大量电能,消耗每千度电产生利润与电价是一次函数关系,经过测算,工厂每千度电产生利润y(元/千度))与电价x(元/千度)的函数图象如图:
(1)请求出y与x之间的函数关系式;
(2)为了实现节能减排目标,有关部门规定,该厂电价x(元/千度)与每天用电量m(千度)的函数关系为x=20m+500,且该工厂每天用电量不超过50千度,为了获得最大利润w,工厂每天应安排使用多少度电?工厂每天消耗电产生利润最大是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分6分)某公司调查某中学学生对其环保产品的了解情况,随机抽取该校部分学生进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为A、B、C、D.根据调查结果绘制了如下尚不完整的统计图.

(1)本次问卷共随机调查了 名学生,扇形统计图中m= .
(2)请根据数据信息补全条形统计图;
(3)若该校有1000名学生,估计选择“非常了解”、“比较了解”共约有多少人?
相关试题

