【题目】如图,在正方形ABCD中,点E,F分别在边AB,BC上,∠ADE=∠CDF.
(1)求证:AE=CF;
(2)连接DB交EF于点O,延长OB至G,使OG=OD,连接EG,FG,判断四边形DEGF是否是菱形,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)四边形DEGF是菱形.理由见解析.
【解析】试题分析:(1)根据正方形的性质可得AD=CD,∠A=∠C=90°,然后利用“角边角”证明△ADE和△CDF全等,根据全等三角形对应边相等可得AE=CF;
(2)求出BE=BF,再求出DE=DF,再根据到线段两端点距离相等的点在线段的垂直平分线可得BD垂直平分EF,然后根据对角线互相垂直平分的四边形是菱形证明.
试题解析:(1)证明:在正方形ABCD中,AD=CD,∠A=∠C=90°,
在△ADE和△CDF中,
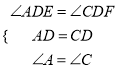 ,
,
∴△ADE≌△CDF(ASA),
∴AE=CF;
(2)四边形DEGF是菱形.
理由如下:在正方形ABCD中,AB=BC,
∵AE=CF,
∴AB﹣AE=BC﹣CF,
即BE=BF,
∵△ADE≌△CDF,
∴DE=DF,
∴BD垂直平分EF,
又∵OG=OD,
∴四边形DEGF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=
 图像的一部分 .其对称轴为x=-1,且过点(-3,0).下列说法:(1)abc<0;(2)2a-b=0;(3)4a+2b+c=0;(4)若(-5,
图像的一部分 .其对称轴为x=-1,且过点(-3,0).下列说法:(1)abc<0;(2)2a-b=0;(3)4a+2b+c=0;(4)若(-5, ),(
),( ,
,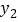 )是抛物线上两点,则
)是抛物线上两点,则 >
>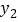 。其中说法正确的是__________(填序号)
。其中说法正确的是__________(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校九年级学生举行朗诵比赛,全年级学生都参加,学校对表现优异的学生进行表彰,设置一、二、三等奖各进步奖共四个奖项,赛后将九年级(1)班的获奖情况绘制成如图所示的两幅不完整的统计图,请根据图中的信息,解答下列问题:

(1)九年级(1)班共有 名学生;
(2)将条形图补充完整:在扇形统计图中,“二等奖”对应的扇形的圆心角度数是 ;
(3)如果该九年级共有1250名学生,请估计荣获一、二、三等奖的学生共有多少名.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列说法:①直径是圆中最长的弦;②等弧所对的弦相等;③圆中90°的角所对的弦是直径;④相等的圆心角对的弧相等.其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=90°﹣∠B,④∠A=∠B=
 ∠C中,能确定△ABC是直角三角形的条件有( )
∠C中,能确定△ABC是直角三角形的条件有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程x2-3x+m=0的一个实数根是1,则m的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x+a>ax+1的解集为x>1,则a的取值范围为( )
A. a<1 B. a>1 C. a>0 D. a<0
相关试题

