【题目】某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?

参考答案:
【答案】(1)y关于x的函数解析式为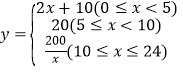 ;(2)恒温系统设定恒温为20°C;(3)恒温系统最多关闭10小时,蔬菜才能避免受到伤害.
;(2)恒温系统设定恒温为20°C;(3)恒温系统最多关闭10小时,蔬菜才能避免受到伤害.
【解析】(1)应用待定系数法分段求函数解析式;
(2)观察图象可得;
(3)代入临界值y=10即可.
(1)设线段AB解析式为y=k1x+b(k≠0)
∵线段AB过点(0,10),(2,14)
代入得![]()
解得![]()
∴AB解析式为:y=2x+10(0≤x<5)
∵B在线段AB上当x=5时,y=20
∴B坐标为(5,20)
∴线段BC的解析式为:y=20(5≤x<10)
设双曲线CD解析式为:y=![]() (k2≠0)
(k2≠0)
∵C(10,20)
∴k2=200
∴双曲线CD解析式为:y=![]() (10≤x≤24)
(10≤x≤24)
∴y关于x的函数解析式为: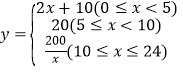
(2)由(1)恒温系统设定恒温为20°C
(3)把y=10代入y=![]() 中,解得,x=20
中,解得,x=20
∴20-10=10
答:恒温系统最多关闭10小时,蔬菜才能避免受到伤害.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售一款口罩,每袋的进价为12元,计划售价大于12元但不超过22元,通过试场调查发现,这种口罩每袋售价提高1元,日均销售量降低5袋,当售价为18元时,日均销售量为50袋.
(1)在售价为18元的基础上,将这种口罩的售价每袋提高x元,则日均销售量是 袋;(用含x的代数式表示)
(2)要想销售这种口罩每天赢利275元,该商场每袋口罩的售价要定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】开学初,李芳和王平去文具店购买学习用品,李芳用18元钱买了1支钢笔和3本笔记本;王平用30元买了同样的钢笔2支和笔记本4本.
(1)求每支钢笔和每本笔记本的价格;
(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔笔记本共36件作为奖品,奖给校运会中表现突出的同学,要求笔记本数不多于钢笔数的2倍,共有多少种购买方案?请你一一写出.
-
科目: 来源: 题型:
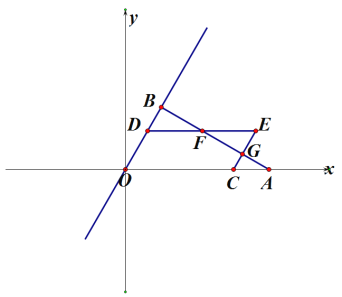
查看答案和解析>>【题目】如图:在平面直角坐标系中,点A在X轴的正半轴,OA=8 ,点B在第一象限,∠AOB=60°,AB⊥OB垂足为B, 点D、C分别在边OB、OA上,且OD=AC=t,以OD、OC为边作平行四边形OCED,DE交直线AB为F,CE交直线AB为点G.
(1) 当t=2时, 则E的坐标为
(2) 若ΔDFC的面积为
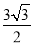 ,求t的值。
,求t的值。(3) 当D、 B 、G、 E四点为顶点的四边形为平行四边形时,在Y轴上存在点M,过点M作FC的平行线交直线OB为点N,若以M、 N、 F、 C为顶点的四边形也是平行四边形,则点M的坐标为 (直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,足球场上守门员在O处开出一高球,球从离地面1m的A处飞出(A在y轴上),运动员乙在距O点6m的B处发现球在自己头的正上方达到最高点M,距地面约4m高.球第一次落地后又弹起.据试验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
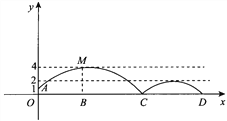
(1)求足球开始飞出到第一次落地时,该抛物线的表达式;
(2)运动员乙要抢到第二个落点D,他应再向前跑多少米?(取
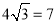 ,
, 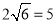 )
) -
科目: 来源: 题型:
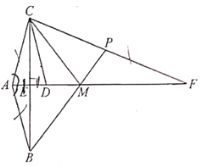
查看答案和解析>>【题目】已知:如图,
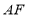 平分
平分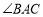 ,
,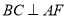 ,垂足为
,垂足为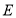 ,点
,点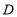 在
在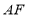 上,
上, ,
,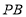 分别与线段
分别与线段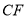 ,
,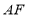 相交于
相交于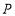 ,
,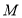 .
.
(1)求证:
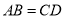 ;
;(2)若
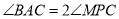 ,请你判断
,请你判断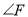 与
与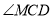 的数量关系,并说明理由.
的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】安九高铁潜山段有甲、乙两个施工队,现中标承建安九高铁一段建设工程.若让两队合作,
 天可以完工,需要费用
天可以完工,需要费用 万元;若让两队合作
万元;若让两队合作 天后,剩下的工程由甲队做,还需
天后,剩下的工程由甲队做,还需 天才能完成,这样只需要费用
天才能完成,这样只需要费用 万元.
万元.(1)甲、乙两队单独完成此项工程各需多少天?
(2)甲、乙两队单独完成此项工程各需费用多少万元?
相关试题

