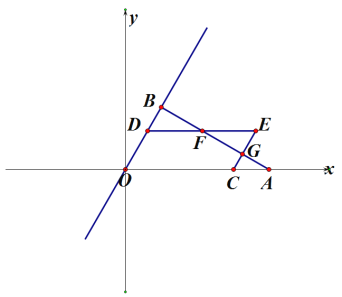
【题目】如图:在平面直角坐标系中,点A在X轴的正半轴,OA=8 ,点B在第一象限,∠AOB=60°,AB⊥OB垂足为B, 点D、C分别在边OB、OA上,且OD=AC=t,以OD、OC为边作平行四边形OCED,DE交直线AB为F,CE交直线AB为点G.
(1) 当t=2时, 则E的坐标为
(2) 若ΔDFC的面积为![]() ,求t的值。
,求t的值。
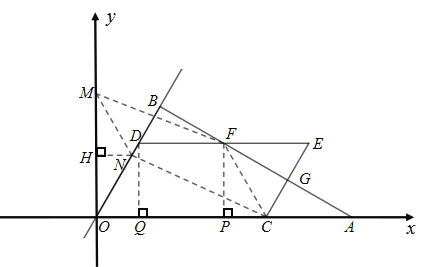
(3) 当D、 B 、G、 E四点为顶点的四边形为平行四边形时,在Y轴上存在点M,过点M作FC的平行线交直线OB为点N,若以M、 N、 F、 C为顶点的四边形也是平行四边形,则点M的坐标为 (直接写出答案)
参考答案:
【答案】(1)(7,![]() );(2)
);(2)![]() ;(3)(0,
;(3)(0,![]() ),(0,
),(0,![]() ).
).
【解析】
(1)根据平行四边形的性质以及勾股定理计算即可;
(2)根据三角形的面积公式,用含t的代数式分别表示出三角形的底和高,列出方程即可;
(3)先根据四边形BDGE是平行四边形计算出t的值;再根据四边形MNCF是平行四边形算出点M的坐标即可.
(1)过点D作DQ⊥OA于点Q,则∠ DQO=90°
当t=2时,OD=AC=2
则OC=OA-AC=8-2=6
在平行四边形OCED中,DE=OC=6
在Rt△OQD中,∠AOB=60°,∠ DQO=90°,
∴![]() ,
,![]()
∴点E的横坐标为:1+6=7,纵坐标为:![]()
故点E的坐标为:(7,![]() )
)
(2)在平行四边形OCED中,CE=OD=t,且OD∥CE,OC∥DE
∵AB⊥OB
∴∠ ABO=90°
又∵OD∥CE
∴∠ AGC=90°,∠ACG=∠AOB=60°,
在Rt△ACG中,∠ACG =60°,∠AGC =90°,
∴![]() ,
,
∴![]()
∴CG=EG
∵OC∥DE
∴∠ACG=∠FEG
在△ACG和△FEG中,
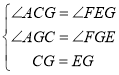
∴△ACG≌△FEG
∴EF=AC=t
∴![]()
由(1)知,![]() ,则
,则![]()
∴![]()
又∵ΔDFC的面积为![]()
∴![]()
解得:![]() ,
,![]()
(3)当点M在y轴正半轴上时;
在Rt△AOB中,∠AOB =60°,∠ABO =90°,
∴![]() ,
,
∴![]()
∵四边形BDGE是平行四边形
∴![]()
∴![]()
由(2)知![]()
∴![]()
解得:![]()
∴![]()
∵OC∥DE,DQ⊥OC,FP⊥OC
∴![]()
若四边形MNCF是平行四边形,
则有MN=CF
有题设条件易得,△CPF≌△NHM
∴![]() ,
,![]()
在Rt△OHN中,∠OHN =90°,∠HON =90°-60°=30°,
∴![]() ,
,
∴![]()
∴点M的坐标为(0,![]() )
)
当点M在y轴负半轴上时;同理可得点M的坐标为(0,![]() )
)
综上所述:点M的坐标为(0,![]() )或(0,
)或(0,![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某政府部门进行公务员招聘考试,其中三人中录取一人,他们的成绩如下:
人
测试成绩
题目
甲
乙
丙
文化课知识
74
87
69
面试
58
74
70
平时表现
87
43
65
(1)按照平均成绩甲、乙、丙谁应被录取?
(2)若按照文化课知识、面试、平时表现的成绩已4:3:1的比例录取,甲、乙、丙谁应被录取?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售一款口罩,每袋的进价为12元,计划售价大于12元但不超过22元,通过试场调查发现,这种口罩每袋售价提高1元,日均销售量降低5袋,当售价为18元时,日均销售量为50袋.
(1)在售价为18元的基础上,将这种口罩的售价每袋提高x元,则日均销售量是 袋;(用含x的代数式表示)
(2)要想销售这种口罩每天赢利275元,该商场每袋口罩的售价要定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】开学初,李芳和王平去文具店购买学习用品,李芳用18元钱买了1支钢笔和3本笔记本;王平用30元买了同样的钢笔2支和笔记本4本.
(1)求每支钢笔和每本笔记本的价格;
(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔笔记本共36件作为奖品,奖给校运会中表现突出的同学,要求笔记本数不多于钢笔数的2倍,共有多少种购买方案?请你一一写出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,足球场上守门员在O处开出一高球,球从离地面1m的A处飞出(A在y轴上),运动员乙在距O点6m的B处发现球在自己头的正上方达到最高点M,距地面约4m高.球第一次落地后又弹起.据试验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
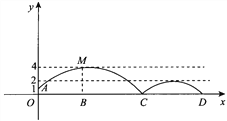
(1)求足球开始飞出到第一次落地时,该抛物线的表达式;
(2)运动员乙要抢到第二个落点D,他应再向前跑多少米?(取
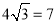 ,
, 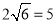 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,
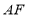 平分
平分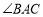 ,
,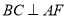 ,垂足为
,垂足为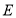 ,点
,点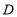 在
在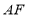 上,
上, ,
,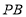 分别与线段
分别与线段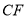 ,
,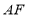 相交于
相交于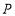 ,
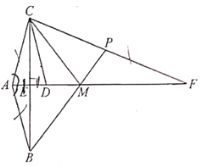
,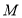 .
.
(1)求证:
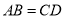 ;
;(2)若
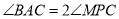 ,请你判断
,请你判断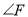 与
与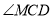 的数量关系,并说明理由.
的数量关系,并说明理由.
相关试题

