【题目】安九高铁潜山段有甲、乙两个施工队,现中标承建安九高铁一段建设工程.若让两队合作,![]() 天可以完工,需要费用
天可以完工,需要费用![]() 万元;若让两队合作
万元;若让两队合作![]() 天后,剩下的工程由甲队做,还需
天后,剩下的工程由甲队做,还需![]() 天才能完成,这样只需要费用
天才能完成,这样只需要费用![]() 万元.
万元.
(1)甲、乙两队单独完成此项工程各需多少天?
(2)甲、乙两队单独完成此项工程各需费用多少万元?
参考答案:
【答案】(1)甲,乙两队单独完成该项工作分别需60,90天;(2)甲、乙两队单独完成此项工程各需费用60万元,360万元.
【解析】
(1)设甲,乙两队单独完成该项工作分别需![]() ,
,![]() 天,根据“若让两队合作,
天,根据“若让两队合作,![]() 天可以完工;若让两队合作
天可以完工;若让两队合作![]() 天后,剩下的工程由甲队做,还需
天后,剩下的工程由甲队做,还需![]() 天才能完成”列出方程组,求解即可;
天才能完成”列出方程组,求解即可;
(2)设甲每天需要费用![]() 万元,乙每天需要费用
万元,乙每天需要费用![]() 万元,根据题意列出方程组,分别求出甲,乙每天需要的费用,结合(1)中结果解答即可.
万元,根据题意列出方程组,分别求出甲,乙每天需要的费用,结合(1)中结果解答即可.
解:(1)设甲,乙两队单独完成该项工作分别需![]() ,
,![]() 天.
天.
由题意得: ,
,
解这个方程组得![]() ,
,
经检验得![]() 是原方程的解
是原方程的解
答:甲,乙两队单独完成该项工程分别需60天,90天;
(2)设甲每天需要费用![]() 万元,乙每天需要费用
万元,乙每天需要费用![]() 万元,
万元,
由题意得:
解得![]()
∴甲单独完成此项工程需费用1×60=60(万元),
乙单独完成此项工程需费用4×90=360(万元),
答:甲、乙两队单独完成此项工程各需费用60万元,360万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,足球场上守门员在O处开出一高球,球从离地面1m的A处飞出(A在y轴上),运动员乙在距O点6m的B处发现球在自己头的正上方达到最高点M,距地面约4m高.球第一次落地后又弹起.据试验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
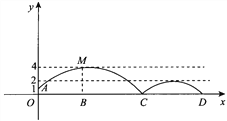
(1)求足球开始飞出到第一次落地时,该抛物线的表达式;
(2)运动员乙要抢到第二个落点D,他应再向前跑多少米?(取
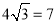 ,
, 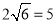 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,
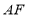 平分
平分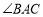 ,
,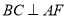 ,垂足为
,垂足为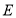 ,点
,点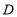 在
在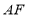 上,
上, ,
,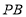 分别与线段
分别与线段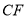 ,
,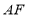 相交于
相交于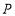 ,
,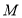 .
.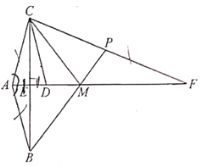
(1)求证:
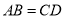 ;
;(2)若
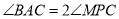 ,请你判断
,请你判断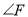 与
与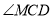 的数量关系,并说明理由.
的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的角满足下列条件:①
的角满足下列条件:① ;②
;② ,
, ;③
;③ ;④
;④ ,
, ,其中一定不是直角三角形的是______.(只填序号)
,其中一定不是直角三角形的是______.(只填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y=
 的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.(1)求k和m的值;
(2)若点C(x,y)也在反比例函数y=
 的图象上,当-3≤x≤-1时,求函数值y的取值范围.
的图象上,当-3≤x≤-1时,求函数值y的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A
 ,B(-1,2)是一次函数
,B(-1,2)是一次函数 与反比例函数
与反比例函数
(
 )图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.

相关试题

