搜索
【题目】如图，△ABC中，E是BC中点，AD是∠BAC的平分线，EF//AD交AC于F．若AB=11，AC=15，则FC的长为（ ）
A.11
B.12
C.13
D.14
参考答案：
【答案】C
【解析】解：∵AD是∠BAC的平分线，AB=11，AC=15，
∴ 
= 
= 
．
∵E是BC中点，
∴ 
= 
= 
．
∵EF//AD，
∴ 
= = ，
∴CF= CA=13．
故选C．
【考点精析】利用平行线的性质和角平分线的性质定理对题目进行判断即可得到答案，需要熟知两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=mx2﹣16mx+48m（m＞0）与x轴交于A，B两点（点B在点A左侧），与y轴交于点C，点D是抛物线上的一个动点，且位于第四象限，连接OD、BD、AC、AD，延长AD交y轴于点E．
（1）若△OAC为等腰直角三角形，求m的值；
（2）若对任意m＞0，C、E两点总关于原点对称，求点D的坐标（用含m的式子表示）；
（3）当点D运动到某一位置时，恰好使得∠ODB=∠OAD，且点D为线段AE的中点，此时对于该抛物线上任意一点P（x0 ， y0）总有n+
≥﹣4 
my02﹣12 y0﹣50成立，求实数n的最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC的面积是12，点D，E，F，G分别是BC，AD，BE，CE的中点，则△AFG的面积是（ ）
A.4.5
B.5
C.5.5
D.6 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2+bx+c经过点（﹣1，0），对称轴l如图所示，则下列结论：①abc＞0；②a﹣b+c=0；③2a+c＜0；④a+b＜0，其中所有正确的结论是（ ）
A.①③
B.②③
C.②④
D.②③④ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，AB=4，点M是OA的中点，过点M的直线与⊙O交于C，D两点．若∠CMA=45°，则弦CD的长为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点E，F在函数y=
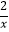的图象上，直线EF分别与x轴、y轴交于点A、B，且BE：BF=1：3，则△EOF的面积是 ． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】学校召集留守儿童过端午节，桌上摆有甲、乙两盘粽子，每盘中盛有白粽2个，豆沙粽1个，肉粽1个（粽子外观完全一样）．
（1）小明从甲盘中任取一个粽子，取到豆沙粽的概率是；
（2）小明在甲盘和乙盘中先后各取了一个粽子，请用树状图或列表法求小明恰好取到两个白粽子的概率．
相关试题
