Question

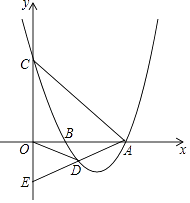
【题目】如图，抛物线y=mx2﹣16mx+48m（m＞0）与x轴交于A，B两点（点B在点A左侧），与y轴交于点C，点D是抛物线上的一个动点，且位于第四象限，连接OD、BD、AC、AD，延长AD交y轴于点E．

（1）若△OAC为等腰直角三角形，求m的值；
（2）若对任意m＞0，C、E两点总关于原点对称，求点D的坐标（用含m的式子表示）；
（3）当点D运动到某一位置时，恰好使得∠ODB=∠OAD，且点D为线段AE的中点，此时对于该抛物线上任意一点P（x0 ， y0）总有n+ ≥﹣4 my02﹣12 y0﹣50成立，求实数n的最小值．

Answer 1

【答案】
（1）

解：令y=mx2﹣16mx+48m=m（x﹣4）（x﹣12）=0，则x1=12，x2=4，

∴A（12，0），即OA=12，

又∵C（0，48m），

∴当△OAC为等腰直角三角形时，OA=OC，

即12=48m，

∴m=

（2）

解：由（1）可知点C（0，48m），

∵对任意m＞0，C、E两点总关于原点对称，

∴必有E（0，﹣48m），

设直线AE的解析式为y=kx+b，

将E（0，﹣48m），A（12，0）代入，可得

，解得 ，

∴直线AE的解析式为y=4mx﹣48m，

∵点D为直线AE与抛物线的交点，

∴解方程组 ，可得 或 （点A舍去），

即点D的坐标为（8，﹣16m）

（3）

解：当∠ODB=∠OAD，∠DOB=∠AOD时，△ODB∽△OAD，

∴OD2=OA×OB=4×12=48，

∴OD=4 ，

又∵点D为线段AE的中点，

∴AE=2OD=8 ，

又∵OA=12，

∴OE= =4 ，

∴D（6，﹣2 ），

把D（6，﹣2 ）代入抛物线y=mx2﹣16mx+48m，可得﹣2 =36m﹣96m+48m，

解得m= ，

∴抛物线的解析式为y= （x﹣4）（x﹣12），

即y= （x﹣8）2﹣ ，

∵点P（x0，y0）为抛物线上任意一点，

∴y0≥﹣ ，

令t=﹣4 my02﹣12 y0﹣50=﹣2y02﹣12 y0﹣50=﹣2（y0+3 ）2+4，

则当y0≥﹣ 时，t最大值=﹣2（﹣ +3 ）2+4= ，

若要使n+ ≥﹣4 my02﹣12 y0﹣50成立，则n+ ≥ ，

∴n≥3 ，

∴实数n的最小值为 ．

【解析】（1）根据y=mx2﹣16mx+48m，可得A（12，0），C（0，48m），再根据OA=OC，即可得到12=48m，进而得出m的值；（2）根据C、E两点总关于原点对称，得到E（0，﹣48m），根据E（0，﹣48m），A（12，0）可得直线AE的解析式，最后解方程组即可得到直线AE与抛物线的交点D的坐标；（3）根据△ODB∽△OAD，可得OD=4 ，进而得到D（6，﹣2 ），代入抛物线y=mx2﹣16mx+48m，可得抛物线解析式，再根据点P（x0 ， y0）为抛物线上任意一点，即可得出y0≥﹣ ，令t=﹣2（y0+3 ）2+4，可得t最大值=﹣2（﹣ +3 ）2+4= ，再根据n+ ≥ ，可得实数n的最小值为 ．
【考点精析】通过灵活运用等腰直角三角形和确定一次函数的表达式，掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法即可以解答此题．