Question

【题目】如图，点E，F在函数y= 的图象上，直线EF分别与x轴、y轴交于点A、B，且BE：BF=1：3，则△EOF的面积是 ．

Answer 1

【答案】
【解析】解：作EP⊥y轴于P，EC⊥x轴于C，FD⊥x轴于D，FH⊥y轴于H，如图所示：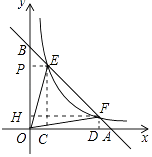

∵EP⊥y轴，FH⊥y轴，
∴EP//FH，
∴△BPE∽△BHF，
∴ = ，即HF=3PE，
设E点坐标为（t， ），则F点的坐标为（3t， ），
∵S△OEF+S△OFD=S△OEC+S梯形ECDF ，
而S△OFD=S△OEC= ×2=1，
∴S△OEF=S梯形ECDF= （ + ）（3t﹣t）= ；
所以答案是： ．
【考点精析】关于本题考查的比例系数k的几何意义，需要了解几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能得出正确答案．