【题目】已知正方形ABCD的边长为2,E为BC边的延长线上一点,CE=2,联结AE,与CD交于点F,联结BF并延长与线段DE交于点G,则BG的长为 .

参考答案:
【答案】![]() .
.
【解析】
试题分析:利用全等三角形的判定AAS得出△ADF≌△ECF,进而得出FG是△DCP的中位线,得出![]() ,再利用勾股定理得出BG的长即可:
,再利用勾股定理得出BG的长即可:
如图,过点C作CP∥BG,交DE于点P.
∵BC=CE=2,∴CP是△BEG的中位线.∴P为EG的中点.
又∵AD=CE=1,AD∥CE,
∴在△ADF和△ECF中,∠AFD=∠EFC,∠ADC=∠FCE,AD=CE,
∴△ADF≌△ECF(AAS).∴CF=DF.
又CP∥FG,∴FG是△DCP的中位线.∴G为DP的中点.
∵CD=CE=2,∴DE=![]() .
.
∴![]() .
.
连接BD,
易知∠BDC=∠EDC=45°,∴∠BDE=90°.
又∵BD=![]()
∴ .
.

-
科目: 来源: 题型:
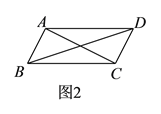
查看答案和解析>>【题目】如图
 ,平行四边形
,平行四边形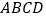 中,对角线
中,对角线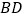 、
、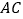 交于点
交于点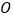 .将直线
.将直线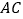 绕点
绕点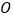 顺时针旋转分别交
顺时针旋转分别交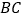 、
、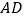 于点
于点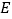 、
、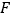 .
.
(
 )在旋转过程中,线段
)在旋转过程中,线段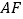 与
与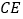 的数量关系是__________.
的数量关系是__________.(
 )如图
)如图 ,若
,若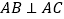 ,当旋转角至少为__________
,当旋转角至少为__________ 时,四边形
时,四边形 是平行四边形,并证明此时的四边形是
是平行四边形,并证明此时的四边形是 是平行四边形.
是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF;EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
(1)求证:四边形EBCF是平行四边形.
(2)若∠BEC=90°,∠ABE=30°,AB=
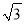 ,求ED的长.
,求ED的长.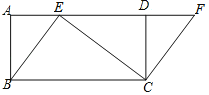
-
科目: 来源: 题型:
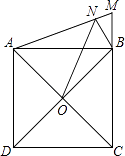
查看答案和解析>>【题目】如图,正方形ABCD的边长为3,延长CB到点M,使BM=1,连接AM,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与x、y轴交于点A(1,0),B(0,﹣1)与反比例函数y=
 在第一象限内的图象交于点C,点C的纵坐标为1.
在第一象限内的图象交于点C,点C的纵坐标为1. 
(1)求一次函数的解析式;
(2)求点C的坐标及反比例函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=90°,
连结AC、EF.在图中找一个与△FAE全等的三角形,并加以证明.

相关试题

