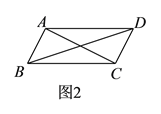
【题目】如图![]() ,平行四边形
,平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() .将直线
.将直线![]() 绕点
绕点![]() 顺时针旋转分别交
顺时针旋转分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.

(![]() )在旋转过程中,线段
)在旋转过程中,线段![]() 与
与![]() 的数量关系是__________.
的数量关系是__________.
(![]() )如图
)如图![]() ,若
,若![]() ,当旋转角至少为__________
,当旋转角至少为__________![]() 时,四边形
时,四边形![]() 是平行四边形,并证明此时的四边形是
是平行四边形,并证明此时的四边形是![]() 是平行四边形.
是平行四边形.
参考答案:
【答案】(![]() )相等;(
)相等;(![]() )
)![]()
【解析】试题分析:(1)根据平行四边形的对边平行可得AD∥BC,对角线互相平分可得OA=OC,再根据两直线平行,内错角相等求出∠1=∠2,然后利用“角边角”证明△AOF和△COE全等,根据全等三角形对应边相等即可得到AF=CE
(2)根据垂直的定义可得∠BAO=90°,然后求出∠BAO=∠AOF,再根据内错角相等,两直线平行可得AB∥EF,然后根据平行四边形的对边平行求出AF∥BE,再根据两组对边分别平行的四边形是平行四边形证明;
试题解析:
(![]() )相等,理由如下:
)相等,理由如下:
如图所示:
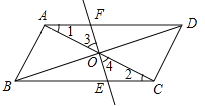
在ABCD中,AD∥BC,OA=OC,
∴∠1=∠2,
在△AOF和△COE中,
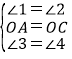
∴△AOF≌△COE(ASA),
∴AF=CE;
(![]() )证明:当旋转角为
)证明:当旋转角为![]() 时,
时,
![]() ,
,
又∵AB⊥AC,
∴∠BAO=90°,
∠AOF=90°,
∴∠BAO=∠AOF,
∴AB∥EF,
∵四边形ABCD是平行四边形,
∴AD∥BC,
即:AF∥BE,
∵AB∥EF,AF∥BE,
∴四边形ABEF是平行四边形;
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题.
 程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).在《算法统宗》里记载了一道趣题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
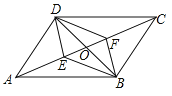
A. AE=CF B. DE=BF C. ∠ADE=∠CBF D. ∠AED=∠CFB
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=
 AC,连接CE,OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )
AC,连接CE,OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( ) 
A.
B.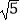
C.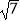
D.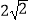
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF;EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
(1)求证:四边形EBCF是平行四边形.
(2)若∠BEC=90°,∠ABE=30°,AB=
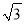 ,求ED的长.
,求ED的长.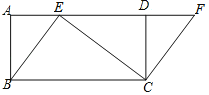
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD的边长为2,E为BC边的延长线上一点,CE=2,联结AE,与CD交于点F,联结BF并延长与线段DE交于点G,则BG的长为 .

相关试题

