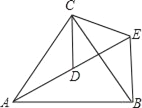
【题目】如图,△ACB和△ECD都是等边三角形,点A、D、E在同一直线上,连接BE.
(1)求证:AD=BE;
(2)求∠AEB的度数.
参考答案:
【答案】(1)证明见解析;(2)∠AEB=60°.
【解析】(1)根据等边三角形的性质得出AC=BC,CD=CE,∠ACB=∠DCE=60°,求出∠ACD=∠BCE,然后根据SAS证明△ACD≌△BCE,即可得出AD=BE;
(2)由△ECD是等边三角形可得∠CDE=∠CED=60°,根据补角的性质可求∠ADC=120°,根据全等三角形的性质可得∠BEC=∠ADC=120°,进而根据∠AEB=∠BEC﹣∠CED可得出答案.
证明:(1)∵△ACB和△ECD都是等边三角形,
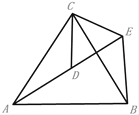
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
又∵∠ACD=∠ACB﹣∠DCB,∠BCE=∠DCE﹣∠DCB,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
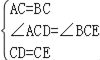
∴△ACD≌△BCE(SAS).
∴AD=BE;
(2)在等边△ECD中,
∠CDE=∠CED=60°,
∴∠ADC=120°,
∵△ACD≌△BCE,
∴∠BEC=∠ADC=120°,
∴∠AEB=∠BEC﹣∠CED=120°﹣60°=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,我们定义点P(a,b)的“变换点”为Q.且规定:当a≥b时,Q为(b,﹣a);当a<b时,Q为(a,﹣b).
(1)点(2,1)的变换点坐标为;
(2)若点A(a,﹣2)的变换点在函数y=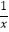 的图象上,求a的值;
的图象上,求a的值;
(3)已知直线l与坐标轴交于(6,0),(0,3)两点.将直线l上所有点的变换点组成一个新的图形记作M. 判断抛物线y=x2+c与图形M的交点个数,以及相应的c的取值范围,请直接写出结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1)
(1)在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称;
(2)写出点A′B′C′的坐标;
(3)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,BC⊥AF于点C,∠A+∠1=90°.
(1)求证:AB∥DE;
(2)如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB,PE.则∠ABP,∠DEP,∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A,D,C重合的情况)?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把长方形纸片OABC放入平面直角坐标系中,使OC、OA分别与x轴,y轴重合,连接OB,将长方形纸片OABC沿OB折叠,使点A落在点A,的位置,A,B与x轴交于D,若点B的坐标为(4,2),则点A,的坐标为( )
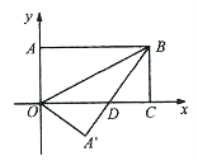
A.
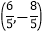 B.
B. 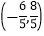 C.
C. 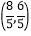 D.
D. 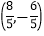
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.

相关试题

