【题目】一个自然数m,若将其数字重新排列可得一个新的自然数n,如果m=3n,我们称m是一个“希望数”.例如:3105=3×1035,71253=3×23751,371250=3×123750.
(1)请说明41不是希望数,并证明任意两位数都不可能是“希望数”.
(2)一个四位“希望数”M记为![]() ,已知
,已知![]() ,且c=2,请求出这个四位“希望数”.
,且c=2,请求出这个四位“希望数”.
参考答案:
【答案】(1)见解析;(2)这个四位“希望数”为7425
【解析】试题分析:(1)根据3×14=42≠41即可得出41不是希望数.
假设存在两位数是希望数,记为![]() ,根据
,根据![]() =3
=3![]() ,即可得出b=1、2、3,逐一分析当b=1、2、3时a的值,验证后即可得出假设不成立,从而得出任意两位数都不可能是“希望数”;
,即可得出b=1、2、3,逐一分析当b=1、2、3时a的值,验证后即可得出假设不成立,从而得出任意两位数都不可能是“希望数”;
(2)根据![]() 可分析出d=0或5,当d=0时可得出a=4,结合c=2即可得出此情况不成立;当d=5时可得出a=7,结合c=2即可得出关于b的一元一次方程,解之即可得出b值,将a、b、c、d值代入该四位数中即可得出结论.
可分析出d=0或5,当d=0时可得出a=4,结合c=2即可得出此情况不成立;当d=5时可得出a=7,结合c=2即可得出关于b的一元一次方程,解之即可得出b值,将a、b、c、d值代入该四位数中即可得出结论.
试题解析:
(1)解:∵3×14=42≠51, ∴41不是希望数.
假设存在两位数是希望数,记为![]() ,
,
∴![]() =3
=3![]() .
.
∵3b为一位数,且b是3a的个位数,
∴b=1,2,3.
当b=1时,a=7,3×17=51≠71;
当b=2时,a=4,3×24=72≠42;
当b=3时,a=1,3×31=93≠13.
综上可知:假设不成立,即任意两位数都不可能是“希望数”
(2)解:∵![]() ,∴3d的个位是d,
,∴3d的个位是d,
∴d=0或5.
当d=0时,∵3a的个位是c,c=2,
∴a=4,
此时3c=6>4,不合适;
当d=5时,∵3a的个位+1是c,c=2,
∴a=7,
又∵![]() ,
,
∴3b+2=10+b,解得:b=4.
∴这个四位“希望数”为7425.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①:在△ABC中,∠ACB=90
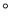 ,△ABC是等腰直角三角形,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.
,△ABC是等腰直角三角形,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.(1)求证:MN=AM+BN.
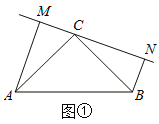
(2)如图②,若过点C在△ABC内作直线MN,AM⊥MN于点M,BN⊥MN于点N,则猜想AM、BN与MN之间有什么关系?请直接写出结论,并写出图②中的全等三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C、D两点在⊙O上,若∠C=45°,
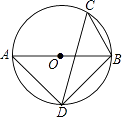
(1)求∠ABD的度数.
(2)若∠CDB=30°,BC=3,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】把5克盐溶于95克水中,盐占盐水的_______% .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)

(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在半径为2的半圆O中,半径OA垂直于直径BC,点E与点F分别在弦AB、AC上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合.
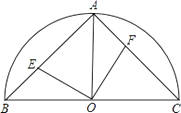
(1)求四边形AEOF的面积.
(2)设AE=x,S△OEF=y,写出y与x之间的函数关系式,求x取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过m(30<m≤100)人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队,收取总费用为y元.
(1)求y关于x的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求m的取值范围.
相关试题

