【题目】如图,AB是⊙O的直径,C、D两点在⊙O上,若∠C=45°, 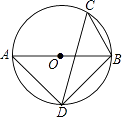
(1)求∠ABD的度数.
(2)若∠CDB=30°,BC=3,求⊙O的半径.
参考答案:
【答案】
(1)解:∵∠C=45°,
∴∠A=∠C=45°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ABD=45°
(2)解:连接AC,
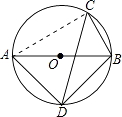
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠CAB=∠CDB=30°,BC=3,
∴AB=6,
∴⊙O的半径为3.
【解析】(1)求出∠A的度数,继而在Rt△ABD中,可求出∠ABD的度数;(2)连接AC,则可得∠CAB=∠CDB=30°,在Rt△ACB中求出AB,继而可得⊙O的半径.
【考点精析】通过灵活运用等腰直角三角形和圆周角定理,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在1个不透明的口袋里,装有红、白、黄三种颜色的乒乓球(除颜色外,其余都相同),其中有白球2个,黄球1个,若从中任意摸出一个球,这个球是白色的概率为0.5.
(1)求口袋中红球的个数;
(2)若摸到红球记0分,摸到白球记1分,摸到黄球记2分,甲从口袋中摸出一个球,不放回,再找出一个画树状图的方法求甲摸的两个球且得2分的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
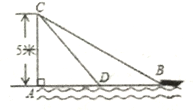
-
科目: 来源: 题型:
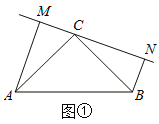
查看答案和解析>>【题目】如图①:在△ABC中,∠ACB=90
 ,△ABC是等腰直角三角形,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.
,△ABC是等腰直角三角形,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.(1)求证:MN=AM+BN.
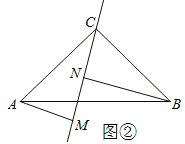
(2)如图②,若过点C在△ABC内作直线MN,AM⊥MN于点M,BN⊥MN于点N,则猜想AM、BN与MN之间有什么关系?请直接写出结论,并写出图②中的全等三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把5克盐溶于95克水中,盐占盐水的_______% .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个自然数m,若将其数字重新排列可得一个新的自然数n,如果m=3n,我们称m是一个“希望数”.例如:3105=3×1035,71253=3×23751,371250=3×123750.
(1)请说明41不是希望数,并证明任意两位数都不可能是“希望数”.
(2)一个四位“希望数”M记为
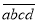 ,已知
,已知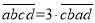 ,且c=2,请求出这个四位“希望数”.
,且c=2,请求出这个四位“希望数”. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)

(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
相关试题

