【题目】定义:三角形一边的中线与这边上的高线之比称为这边上的中高比.
(1)直接写出等腰直角三角形腰上的中高比为 .
(2)已知一个直角三角形一边上的中高比为5:4,求它的最小内角的正切值.
(3)如图,已知函数y= ![]() (x+4)(x﹣m)与x轴交于A、B两点,与y轴的负半轴交于点C,对称轴与x的正半轴交于点D,若△ABC中AB边上的中高比为5:4,求m的值.
(x+4)(x﹣m)与x轴交于A、B两点,与y轴的负半轴交于点C,对称轴与x的正半轴交于点D,若△ABC中AB边上的中高比为5:4,求m的值.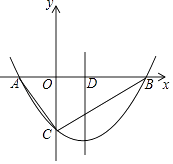
参考答案:
【答案】
(1)![]()
(2)
解:①当斜边上的中高比为5:4时,设高线为4k,则此边上的中线为5k,如图2,
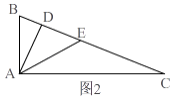
在△ABC中,∠BAC=90°,
∴AD是高,
∴AD=4x,AE是中线,
∴CE=AE=5x,
在RtADE中,DE= ![]() =3k,
=3k,
∴CD=CE+DE=8k,
∴tan∠C= ![]() =
= ![]() =
= ![]() ,
,
当直角边上的中高比为5:4时,设高为4k,此边上的中线为5k,
如图3,
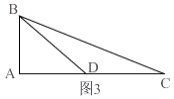
在△ABC中,∠BAC=90°,AB是AC边上的高,为4k,BD为AC边上的中线,为5k,
根据勾股定理得,AD= ![]() =3k,
=3k,
∴AC=2AD=6k,
∴tan∠C= ![]() =
= ![]() ,
,
∴直角三角形的最小内角的正切值为 ![]() 或
或 ![]() ;
;
(3)
解:∵函数y= ![]() (x+4)(x﹣m)与x轴交于A、B两点,
(x+4)(x﹣m)与x轴交于A、B两点,
∴令y=0,∴0= ![]() (x+4)(x﹣m),
(x+4)(x﹣m),
∴x=﹣4或x=m,
∴A(﹣4,0),B(m,0),
∵点C是抛物线与y轴的交点,
∴C(0,﹣ ![]() ),
),
∵对称轴与x的正半轴交于点D,
∴D( ![]() ,0),
,0),
在Rt△COD中,设CD=5k,
∴OC=4k,
根据勾股定理得,OD=3k,
∴ 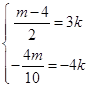 ,∴
,∴ ![]() ,
,
即m的值为10.
【解析】解:(1)如图1,
设等腰直角三角形的直角边为2x,
∴BC边上的高为AB=2x,
∵AD是BC边上的中线,
∴BD= ![]() BC=x,
BC=x,
在Rt△ABD中,根据勾股定理得,AD= ![]() =
= ![]() x,
x,
∴等腰直角三角形腰上的中高比为 ![]() =
= ![]() ,
,
所以答案是: ![]() ;
;
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
我们定义:如果一个数的平方等于﹣1,记作i2=﹣1,那么这个i就叫做虚数单位.虚数与我们学过的实数合在一起叫做复数.一个复数可以表示为a+bi(a,b均为实数)的形式,其中a叫做它的实部,b叫做它的虚部.
复数的加、减、乘的运算与我们学过的整式加、减、乘的运算类似.
例如 计算:(5+i)+(3﹣4i)=(5+3)+(i﹣4i)=8﹣3i.
根据上述材料,解决下列问题:
(1)填空:i3= ,i4= ;
(2)计算:(2+i)2;
(3)将
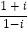 化为a+bi(a,b均为实数)的形式(即化为分母中不含i的形式).
化为a+bi(a,b均为实数)的形式(即化为分母中不含i的形式). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABGD中,AB=AD=6,梯形ABCD中,DE⊥DC交AB于E,DF平分∠EDC交BC于F,连结EF.

(1)证明:EF=CF;
(2)当 时,求EF的长.
时,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,圆D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.
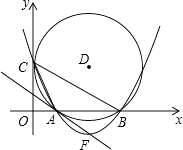
(1)则D点的坐标是 ( , ),圆的半径为;
(2)sin∠ACB=;经过C、A、B三点的抛物线的解析式;
(3)设抛物线的顶点为F,证明直线FA与圆D相切;
(4)在x轴下方的抛物线上,是否存在一点N,使△CBN面积最大,最大值是多少,并求出N点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,∠CAB=90°,AB=AC.
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上两动点(不与B,C重合),点P在点Q左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小明通过观察和实验,提出猜想:在点P,Q运动的过程中,始终有PM=
 PA.他把这个猜想与同学们进行交流,通过讨论,形成以下证明猜想的思路:
PA.他把这个猜想与同学们进行交流,通过讨论,形成以下证明猜想的思路:(Ⅰ)要想证明PM=
 PA,只需证△APM为等腰直角三角形;
PA,只需证△APM为等腰直角三角形;(Ⅱ)要想证明△APM为等腰直角三角形,只需证∠PAM=90°,PA=AM;
…
请参考上面的思路,帮助小明证明PM=
 PA.
PA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知:点A(0,0),B(
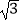 ,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …,则第n个等边三角形的边长等于 .
,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …,则第n个等边三角形的边长等于 . 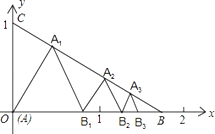
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数
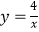 的图象经过点C,且与AB交于点E.若OD=2,则△OAE的面积为 .
的图象经过点C,且与AB交于点E.若OD=2,则△OAE的面积为 . 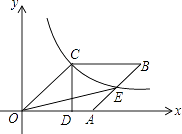
相关试题

