【题目】已知:在△ABC中,∠CAB=90°,AB=AC.
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上两动点(不与B,C重合),点P在点Q左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小明通过观察和实验,提出猜想:在点P,Q运动的过程中,始终有PM=![]() PA.他把这个猜想与同学们进行交流,通过讨论,形成以下证明猜想的思路:
PA.他把这个猜想与同学们进行交流,通过讨论,形成以下证明猜想的思路:
(Ⅰ)要想证明PM=![]() PA,只需证△APM为等腰直角三角形;
PA,只需证△APM为等腰直角三角形;
(Ⅱ)要想证明△APM为等腰直角三角形,只需证∠PAM=90°,PA=AM;
…
请参考上面的思路,帮助小明证明PM=![]() PA.
PA.

参考答案:
【答案】(1)∠AQB=65°;(2)①详见解析;②详见解析.
【解析】
(1)首先证明∠BAP=∠CAQ,再根据三角形的外角的性质计算即可;
(2)①根据要求画出图形即可;
②只要证明AP=AM,∠PAM=90°即可解决问题;
(1)解:如图1中,
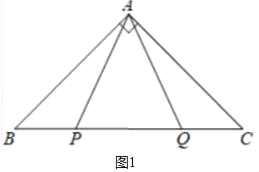
∵AB=AC,∠BAC=90°
∴∠B=∠C=45°
∵AP=AQ,
∴∠APQ=∠AQC,
∵∠APQ=∠B+∠BAP,∠AQP=∠C+∠CAQ,
∴∠BAP=∠CAQ=20°,
∴∠AQB=45°+20°=65°.
(2)①解:如图2中所示:
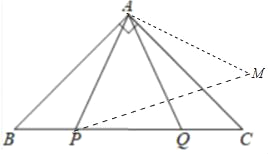
②证明:∵Q、M关于AC对称,
∴AQ=AM,∠QAC=∠MAC,
∵∠BAP=∠CAQ,
∴∠BAP=∠CAM,
∴∠BAP+∠PAC=∠CAM+∠PAC,
即∠PAM=∠BAC=90°,
∵AP=AQ,
∴AP=AM,
∴△PAM是等腰直角三角形,
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABGD中,AB=AD=6,梯形ABCD中,DE⊥DC交AB于E,DF平分∠EDC交BC于F,连结EF.

(1)证明:EF=CF;
(2)当 时,求EF的长.
时,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,圆D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.
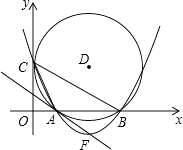
(1)则D点的坐标是 ( , ),圆的半径为;
(2)sin∠ACB=;经过C、A、B三点的抛物线的解析式;
(3)设抛物线的顶点为F,证明直线FA与圆D相切;
(4)在x轴下方的抛物线上,是否存在一点N,使△CBN面积最大,最大值是多少,并求出N点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:三角形一边的中线与这边上的高线之比称为这边上的中高比.
(1)直接写出等腰直角三角形腰上的中高比为 .
(2)已知一个直角三角形一边上的中高比为5:4,求它的最小内角的正切值.
(3)如图,已知函数y=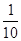 (x+4)(x﹣m)与x轴交于A、B两点,与y轴的负半轴交于点C,对称轴与x的正半轴交于点D,若△ABC中AB边上的中高比为5:4,求m的值.
(x+4)(x﹣m)与x轴交于A、B两点,与y轴的负半轴交于点C,对称轴与x的正半轴交于点D,若△ABC中AB边上的中高比为5:4,求m的值.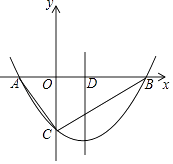
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知:点A(0,0),B(
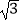 ,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …,则第n个等边三角形的边长等于 .
,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …,则第n个等边三角形的边长等于 . 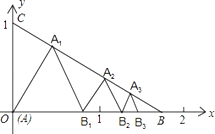
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数
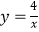 的图象经过点C,且与AB交于点E.若OD=2,则△OAE的面积为 .
的图象经过点C,且与AB交于点E.若OD=2,则△OAE的面积为 . 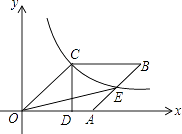
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,A、B在数轴上对应的数分别用a、b表示,且(a﹣20)2+|b+10|=0,P是数轴上的一个动点.
(1)在数轴上标出A、B的位置,并求出A、B之间的距离;
(2)已知线段OB上有点C且|BC|=6,当数轴上有点P满足PB=2PC时,求P点对应的数;
(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,…….点P能移动到与A或B重合的位置吗?若不能,请直接回答;若能,请直接指出,第几次移动,与哪一点重合.
相关试题

