【题目】如图,在平面直角坐标系xOy中,已知反比例函数![]() 与一次函数y=ax+b(a≠0)的图象相交于点A(1,8)和B(4,m).
与一次函数y=ax+b(a≠0)的图象相交于点A(1,8)和B(4,m).
(1)分别求反比例函数和一次函数的表达式;
(2)过动点P(n,0)且垂直于x轴的直线分别与反比例函数图象和一次函数图象交于C、D两点,当点C位于点D下方时,直接写出n的取值范围.

参考答案:
【答案】(1)反比例函数表达式为![]() ,一次函数表达式为y=﹣2x+10;(2)n的取值范围是1<n<4.
,一次函数表达式为y=﹣2x+10;(2)n的取值范围是1<n<4.
【解析】分析:(1)把A代入反比例函数的解析式即可求得k的值,然后求得B的值,利用待定系数法即可求得一次函数的解析式;
(2)先画出两函数的图象,再根据两函数图象的上下位置关系结合交点的横坐标即可得出n的取值范围.
本题解析:
(1)∵点A(1,8)和B(4,m)在反比例函数![]() 的图象上,
的图象上,
∴k=8,m=2.
∴反比例函数表达式为![]() .
.
点B的坐标为B(4,2).
∵点A(1,8)和B(4,2)在一次函数y=ax+b的图象上,
∴![]() 解得
解得![]()
∴一次函数表达式为y=﹣2x+10;
(2)一次函数y=﹣2x+10(a≠0)的图象相交于点A(1,8)和B(4,2).
观察函数图象可知:若过动点P(n,0)且垂直于x轴的直线分别与反比例函数图象和一次函数图象交于C、D两点,当点C位于点D下方时
则n的取值范围是1<n<4.

点睛:本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征及待定系数法求函数解析式,根据两函数图象的上下位置关系找出不等式的解集是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,(1)正方形ABCD及等腰Rt△AEF有公共顶点A,∠EAF=90°, 连接BE、DF.将Rt△AEF绕点A旋转,在旋转过程中,BE、DF具有怎样的数量关系和位置关系?结合图(1)给予证明;
(2)将(1)中的正方形ABCD变为矩形ABCD,等腰Rt△AEF变为Rt△AEF,且AD=kAB,AF=kAE,其他条件不变.(1)中的结论是否发生变化?结合图(2)说明理由;
(3)将(2)中的矩形ABCD变为平行四边形ABCD,将Rt△AEF变为△AEF,且∠BAD=∠EAF=
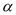 ,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用
,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用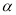 表示出直线BE、DF形成的锐角
表示出直线BE、DF形成的锐角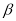 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两张完全相同的长方形纸片(长为12,宽为4)如图叠放在一起,重叠部分为四边形ABCD,则四边形ABCD的周长最大值为____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,我们规定:点
 关于“
关于“ 的衍生点”,
的衍生点”, ,其中
,其中 为常数且
为常数且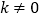 ,如:点
,如:点 (
( ,
, )关于“
)关于“ 的衍生点”,即
的衍生点”,即 ,即
,即 .
.(1)求点
 关于“
关于“ 的衍生点”
的衍生点”  的坐标;
的坐标;(2)若点
 关于“
关于“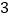 的衍生点”
的衍生点”  ,求点
,求点 的坐标;
的坐标;(3)若点
 在
在 轴的正半轴上,点
轴的正半轴上,点 关于“
关于“ 的衍生点”
的衍生点”  ,点
,点 关于“
关于“ 的衍生点”
的衍生点”  ,且线段
,且线段 的长度不超过线段
的长度不超过线段 长度的一半,请问:是否存在
长度的一半,请问:是否存在 值使得
值使得 到
到 轴的距离是
轴的距离是 到
到 轴距离的
轴距离的 倍?若存在,请求出
倍?若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知长方形
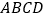 ,点
,点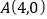 ,
,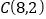 .
.(1)如图,有一动点
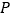 在第二象限的角平分线
在第二象限的角平分线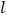 上,若
上,若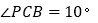 ,求
,求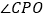 的度数;
的度数;(2)若把长方形
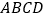 向上平移,得到长方形
向上平移,得到长方形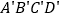 .
.①在运动过程中,求
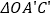 的面积与
的面积与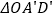 的面积之间的数量关系;
的面积之间的数量关系;②若
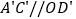 ,求
,求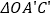 的面积与
的面积与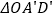 的面积之比.
的面积之比. 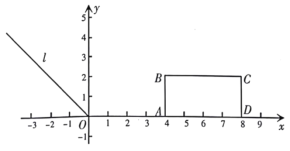
-
科目: 来源: 题型:
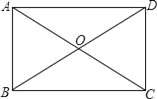
查看答案和解析>>【题目】如图,ABCD的对角线AC,BD相交于点O,△OAB是等边三角形.
(1)求证:ABCD为矩形;
(2)若AB=4,求ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,每一个小方格的边个长为1个单位.

(1)请写出△ABC各点的坐标;
(2)若把△ABC向上平移2个单位,再向右平移2个单位得到△A1B1C1,在图中画出△A1B1C1;
(3)求△A1B1C1的面积.
相关试题

