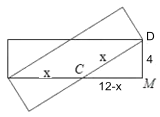
【题目】如图,两张完全相同的长方形纸片(长为12,宽为4)如图叠放在一起,重叠部分为四边形ABCD,则四边形ABCD的周长最大值为____.

参考答案:
【答案】![]()
【解析】
首先可判断重叠部分为平行四边形,且两条纸条宽度相同;再由平行四边形的面积可得邻边相等,则重叠部分为菱形;设菱形的边长为x,根据勾股定理求出周长即可.
解答:解:由题意得:AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∵用两张等宽的纸条交叉叠放在一起,重叠部分为四边形ABCD,
SABCD=BC×宽=CD×宽,
∴BC=CD,
∴四边形ABCD是菱形.
当两张纸条如图所示放置时,菱形周长最大,
设这时菱形的边长为xcm,
在Rt△MBD中,
由勾股定理:x2=(12x)2+42,
解得:x=![]() ,
,
∴4x=![]() ,
,
即菱形的最大周长为![]() cm.
cm.
故答案为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为△ABC中∠ BAC的外角平分线,BD⊥AD于D,E为BC中点,DE=5,AC=3,则AB长为()

A.8.5B.8C.7.5D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0, d)、C(-3,2).
(1)求d的值;
(2)将△ABC沿
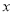 轴的正方向平移a个单位,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上.请求出这个反比例函数和此时直线B′C′的解析式;
轴的正方向平移a个单位,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上.请求出这个反比例函数和此时直线B′C′的解析式;(3)在(2)的条件下,直线
 交y轴于点G,作
交y轴于点G,作 ⊥
⊥ 轴于
轴于 .
.  是线段
是线段 上的一点,若△
上的一点,若△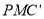 和△
和△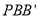 面积相等,求点
面积相等,求点 坐标.
坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,(1)正方形ABCD及等腰Rt△AEF有公共顶点A,∠EAF=90°, 连接BE、DF.将Rt△AEF绕点A旋转,在旋转过程中,BE、DF具有怎样的数量关系和位置关系?结合图(1)给予证明;
(2)将(1)中的正方形ABCD变为矩形ABCD,等腰Rt△AEF变为Rt△AEF,且AD=kAB,AF=kAE,其他条件不变.(1)中的结论是否发生变化?结合图(2)说明理由;
(3)将(2)中的矩形ABCD变为平行四边形ABCD,将Rt△AEF变为△AEF,且∠BAD=∠EAF=
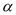 ,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用
,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用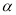 表示出直线BE、DF形成的锐角
表示出直线BE、DF形成的锐角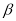 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,我们规定:点
 关于“
关于“ 的衍生点”,
的衍生点”, ,其中
,其中 为常数且
为常数且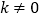 ,如:点
,如:点 (
( ,
, )关于“
)关于“ 的衍生点”,即
的衍生点”,即 ,即
,即 .
.(1)求点
 关于“
关于“ 的衍生点”
的衍生点”  的坐标;
的坐标;(2)若点
 关于“
关于“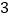 的衍生点”
的衍生点”  ,求点
,求点 的坐标;
的坐标;(3)若点
 在
在 轴的正半轴上,点
轴的正半轴上,点 关于“
关于“ 的衍生点”
的衍生点”  ,点
,点 关于“
关于“ 的衍生点”
的衍生点”  ,且线段
,且线段 的长度不超过线段
的长度不超过线段 长度的一半,请问:是否存在
长度的一半,请问:是否存在 值使得
值使得 到
到 轴的距离是
轴的距离是 到
到 轴距离的
轴距离的 倍?若存在,请求出
倍?若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知反比例函数
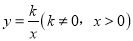 与一次函数y=ax+b(a≠0)的图象相交于点A(1,8)和B(4,m).
与一次函数y=ax+b(a≠0)的图象相交于点A(1,8)和B(4,m).(1)分别求反比例函数和一次函数的表达式;
(2)过动点P(n,0)且垂直于x轴的直线分别与反比例函数图象和一次函数图象交于C、D两点,当点C位于点D下方时,直接写出n的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知长方形
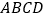 ,点
,点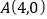 ,
,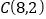 .
.(1)如图,有一动点
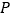 在第二象限的角平分线
在第二象限的角平分线 上,若
上,若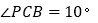 ,求
,求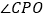 的度数;
的度数;(2)若把长方形
 向上平移,得到长方形
向上平移,得到长方形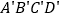 .
.①在运动过程中,求
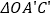 的面积与
的面积与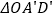 的面积之间的数量关系;
的面积之间的数量关系;②若
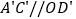 ,求
,求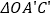 的面积与
的面积与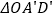 的面积之比.
的面积之比. 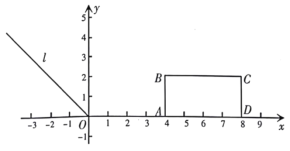
相关试题

