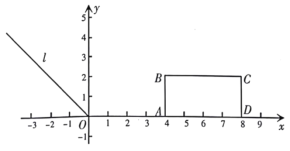
【题目】在平面直角坐标系中,已知长方形![]() ,点
,点![]() ,
,![]() .
.
(1)如图,有一动点![]() 在第二象限的角平分线
在第二象限的角平分线![]() 上,若
上,若![]() ,求
,求![]() 的度数;
的度数;
(2)若把长方形![]() 向上平移,得到长方形
向上平移,得到长方形![]() .
.
①在运动过程中,求![]() 的面积与
的面积与![]() 的面积之间的数量关系;
的面积之间的数量关系;
②若![]() ,求
,求![]() 的面积与
的面积与![]() 的面积之比.
的面积之比.
参考答案:
【答案】(1)55°或35°;(2)①![]() ;②
;②![]() .
.
【解析】
(1)分两种情况:①在Rt△FEC中,求出∠FEC=90°-10°=80°,然后根据点![]() 在第二象限的角平分线
在第二象限的角平分线![]() 上,得出∠POE=45°,对顶角相等,即可得出∠CPO=180°-80°-45°=55°;②由已知条件,得出∠CEO=45°,又根据∠CEO=∠CPE+∠PCB,得出∠CPO;
上,得出∠POE=45°,对顶角相等,即可得出∠CPO=180°-80°-45°=55°;②由已知条件,得出∠CEO=45°,又根据∠CEO=∠CPE+∠PCB,得出∠CPO;
(2)①首先设长方形![]() 向上平移
向上平移![]() 个单位长,得到长方形
个单位长,得到长方形![]() ,然后列出
,然后列出![]() 和
和![]() 的面积,即可得出两者的数量关系;
的面积,即可得出两者的数量关系;
②首先根据已知条件判定四边形![]() 是平行四边形,经过等量转化,即可得出
是平行四边形,经过等量转化,即可得出![]() 和
和![]() 的面积,进而得出其面积之比.
的面积,进而得出其面积之比.
(1)分两种情况:
①令PC交x轴于点E,延长CB至x轴,交于点F,如图所示:
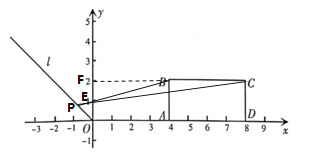
由已知得,![]() ,∠CFE=90°
,∠CFE=90°
∴∠FEC=90°-10°=80°,
又∵点![]() 在第二象限的角平分线
在第二象限的角平分线![]() 上,
上,
∴∠POE=45°
又∵∠FEC=∠PEO=80°
∴∠CPO=180°-80°-45°=55°
②延长CB,交直线l于点E,
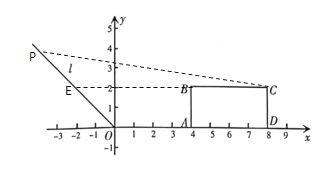
由已知得,![]() ,
,
∵点![]() 在第二象限的角平分线
在第二象限的角平分线![]() 上,
上,
∴∠CEO=45°
∴∠CEO=∠CPE+∠PCB
∴∠CPO=45°-10°=35°.
故答案为55°或35°.
(2)如图,
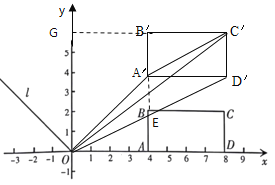
①设长方形![]() 向上平移
向上平移![]() 个单位长,得到长方形
个单位长,得到长方形![]()
![]()
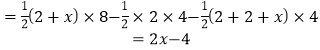
![]()
∴![]()
②∵长方形![]() ,
,
∴![]()
∵![]() ,
,
令![]() 交
交![]() 于E,
于E,
则四边形![]() 是平行四边形,
是平行四边形,
∴![]()
∴![]()
又∵![]()
由①得知,![]()
∴![]()
![]()
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两张完全相同的长方形纸片(长为12,宽为4)如图叠放在一起,重叠部分为四边形ABCD,则四边形ABCD的周长最大值为____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,我们规定:点
 关于“
关于“ 的衍生点”,
的衍生点”, ,其中
,其中 为常数且
为常数且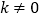 ,如:点
,如:点 (
( ,
, )关于“
)关于“ 的衍生点”,即
的衍生点”,即 ,即
,即 .
.(1)求点
 关于“
关于“ 的衍生点”
的衍生点”  的坐标;
的坐标;(2)若点
 关于“
关于“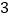 的衍生点”
的衍生点”  ,求点
,求点 的坐标;
的坐标;(3)若点
 在
在 轴的正半轴上,点
轴的正半轴上,点 关于“
关于“ 的衍生点”
的衍生点”  ,点
,点 关于“
关于“ 的衍生点”
的衍生点”  ,且线段
,且线段 的长度不超过线段
的长度不超过线段 长度的一半,请问:是否存在
长度的一半,请问:是否存在 值使得
值使得 到
到 轴的距离是
轴的距离是 到
到 轴距离的
轴距离的 倍?若存在,请求出
倍?若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知反比例函数
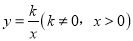 与一次函数y=ax+b(a≠0)的图象相交于点A(1,8)和B(4,m).
与一次函数y=ax+b(a≠0)的图象相交于点A(1,8)和B(4,m).(1)分别求反比例函数和一次函数的表达式;
(2)过动点P(n,0)且垂直于x轴的直线分别与反比例函数图象和一次函数图象交于C、D两点,当点C位于点D下方时,直接写出n的取值范围.

-
科目: 来源: 题型:
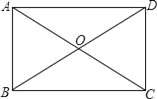
查看答案和解析>>【题目】如图,ABCD的对角线AC,BD相交于点O,△OAB是等边三角形.
(1)求证:ABCD为矩形;
(2)若AB=4,求ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,每一个小方格的边个长为1个单位.

(1)请写出△ABC各点的坐标;
(2)若把△ABC向上平移2个单位,再向右平移2个单位得到△A1B1C1,在图中画出△A1B1C1;
(3)求△A1B1C1的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,E为对角线BD的延长线上一点.

(1)求证:AE=CE.
(2)若BC=6,AE=10,∠BAE=120,求BE的长,并直接写出DE的长为 .
相关试题

