【题目】如图所示,每一个小方格的边个长为1个单位.

(1)请写出△ABC各点的坐标;
(2)若把△ABC向上平移2个单位,再向右平移2个单位得到△A1B1C1,在图中画出△A1B1C1;
(3)求△A1B1C1的面积.
参考答案:
【答案】(1)A(﹣2,3),B(1,0),C(5,0);(2)详见解析;(3)6.
【解析】
(1)直接通过题图即可得解;
(2)根据“上加下减横不变,左减右加纵不变”得到平移后的顶点坐标,然后描点连线即可;
(3)根据三角形的面积公式求解即可.
解:(1)由图可得,A(﹣2,3),B(1,0),C(5,0);
(2)根据题意平移后三角形顶点坐标为:A1(0,5),B1(3,2),C1(7,2),
如图所示,△A1B1C1即为所求;
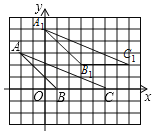
(3)△A1B1C1的面积为![]() ×4×3=6.
×4×3=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知反比例函数
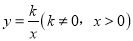 与一次函数y=ax+b(a≠0)的图象相交于点A(1,8)和B(4,m).
与一次函数y=ax+b(a≠0)的图象相交于点A(1,8)和B(4,m).(1)分别求反比例函数和一次函数的表达式;
(2)过动点P(n,0)且垂直于x轴的直线分别与反比例函数图象和一次函数图象交于C、D两点,当点C位于点D下方时,直接写出n的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知长方形
 ,点
,点 ,
,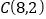 .
.(1)如图,有一动点
 在第二象限的角平分线
在第二象限的角平分线 上,若
上,若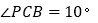 ,求
,求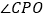 的度数;
的度数;(2)若把长方形
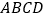 向上平移,得到长方形
向上平移,得到长方形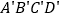 .
.①在运动过程中,求
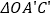 的面积与
的面积与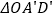 的面积之间的数量关系;
的面积之间的数量关系;②若
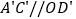 ,求
,求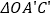 的面积与
的面积与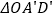 的面积之比.
的面积之比. 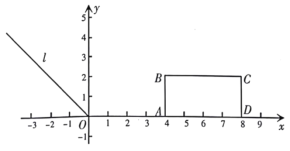
-
科目: 来源: 题型:
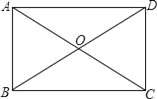
查看答案和解析>>【题目】如图,ABCD的对角线AC,BD相交于点O,△OAB是等边三角形.
(1)求证:ABCD为矩形;
(2)若AB=4,求ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,E为对角线BD的延长线上一点.

(1)求证:AE=CE.
(2)若BC=6,AE=10,∠BAE=120,求BE的长,并直接写出DE的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数y=x﹣
 的图象和性质.
的图象和性质.小石根据学习函数的经验,对此函数的图象和性质进行了探究.
下面是小石的探究过程,请补充完整:
(1)函数的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值,
x
…
﹣3
﹣2
﹣1
﹣

﹣



1
2
3
…
y
…
﹣

﹣1
1
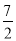

﹣

﹣

m
1

…
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出此函数的图象;
(4)进一步探究,结合函数的图象,写出此函数的性质(一条即可): .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在13×7的网格中,每个小正方形边长都是1,其顶点叫做格点,如图A、B、D、E、M、P均为格点.
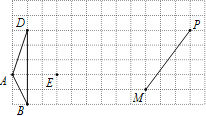
(1)请在网格中画□ABCD,要求C点在格点上.
(2)在(1)中□ABCD右侧画格点△EFG,并使EF=5,FG=3,EG=
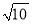 .
.(3)以MP为对角线画矩形MNPQ(M、N、P、Q按逆时针方向排列),使矩形MNPQ的面积为10.
(4)在直线AE上有一点W,使WB+WM的值最小,则这个最小值为 .
相关试题

