【题目】如图,在等边![]() 中,边
中,边![]() 厘米,若动点
厘米,若动点![]() 从点
从点![]() 开始,按
开始,按![]() 的路径运动,且速度为1厘米/秒,设点
的路径运动,且速度为1厘米/秒,设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
(1)当![]() 时,判断
时,判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)当![]() 的面积为
的面积为![]() 面积的一半时,求
面积的一半时,求![]() 的值;
的值;
(3)另有一点![]() ,从点
,从点![]() 开始,按
开始,按![]() 的路径运动,且速度为
的路径运动,且速度为![]() 厘米/秒,若
厘米/秒,若![]() 、
、![]() 两点同时出发,当
两点同时出发,当![]() 、
、![]() 中有一点到达终点时,另一点也停止运动.当
中有一点到达终点时,另一点也停止运动.当![]() 为何值时,直线
为何值时,直线![]() 把
把![]() 的周长分成相等的两部分.
的周长分成相等的两部分.
参考答案:
【答案】(1)![]() ,理由见解析;(2)
,理由见解析;(2)![]() 的值为9或15;(3)当
的值为9或15;(3)当![]() 为
为![]() 或
或![]() 秒时,直线
秒时,直线![]() 把
把![]() 的周长分成相等的两部分.
的周长分成相等的两部分.
【解析】
(1)![]() ,所以
,所以![]() ,而
,而![]() 根据等腰三角形三线合一可得
根据等腰三角形三线合一可得![]() ;
;
(2)分当点![]() 为
为![]() 中点和当点
中点和当点![]() 为
为![]() 中点时分别计算其路程,进而求其时间t;
中点时分别计算其路程,进而求其时间t;
(3)由于点Q从C开始,按![]() 的路径运动,与点P同时出发,且其速度是点P的1.5倍,所以当点Q到达终点C时,点P刚到达点A,即点P只能在线段BC和AB上,故直线PQ把
的路径运动,与点P同时出发,且其速度是点P的1.5倍,所以当点Q到达终点C时,点P刚到达点A,即点P只能在线段BC和AB上,故直线PQ把![]() 的周长分成相等的两部分时分两种情况:当点
的周长分成相等的两部分时分两种情况:当点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上和当点
上和当点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,分别计算求解即可.
上,分别计算求解即可.
解:(1)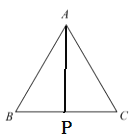
判断:![]() ,
,
理由如下:
因为![]() ,所以
,所以![]()
又因为![]()
所以![]()
(2)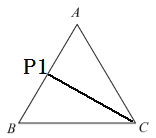
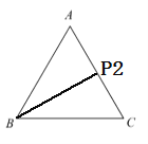
当点![]() 为
为![]() 中点时,显然
中点时,显然![]() ,所以
,所以![]()
当点![]() 为
为![]() 中点时,显然
中点时,显然![]() ,所以
,所以![]()
所以![]() 的值为9或15
的值为9或15
(3)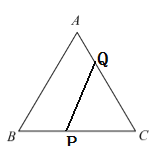
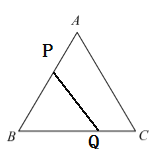
当点![]() 在边
在边![]() 上,且点
上,且点![]() 在边
在边![]() 上时,
上时,![]() ,
,![]()
则![]() ,所以
,所以![]()
当点![]() 在边
在边![]() 上,且点
上,且点![]() 在边
在边![]() 上时,
上时,![]()
![]() ,
,
则![]() ,所以
,所以![]()
所以当![]() 为
为![]() 或
或![]() 秒时,直线
秒时,直线![]() 把
把![]() 的周长分成相等的两部分.
的周长分成相等的两部分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校新到一批理、化、生实验器材需要整理,若实验管理员李老师一人单独整理需要40分钟完成,现在李老师与工人王师傅共同整理20分钟后,李老师因事外出,王师傅再单独整理了20分钟才完成任务.
(1)王师傅单独整理这批实验器材需要多少分钟?
(2)学校要求王师傅的工作时间不能超过30分钟,要完成整理这批器材,李老师至少要工作多少分钟? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,D是边AC上一点,连接BD,使∠A=2∠1,点E是BC上的一点,以BE为直径的⊙O经过点D.
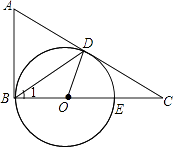
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,以A(2,0),B(0,t)为顶点作等腰直角△ABC(其中∠ABC=90°,且点C落在第一象限内),则点C关于y轴的对称点C’的坐标为___.(用t的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c的顶点D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c>0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根. 其中正确的结论是( )

A.③④
B.②④
C.②③
D.①④ -
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价30元。厂方在开展促销活动期间,向客户提供两种优惠方案:方案一:一套西装送一条领带; 方案二:西装和领带都按定价的90%付款。现某客户要到该服装厂购买西装20套,领带x条(x>20)。
(1)若该客户按方案①购买,需付款 元(用含x的代数式表示);若该客户按方案②购买,需付款 元(用含x的代数式表示)°
(2)若x=30,两种方案中,通过计算说明选择按哪种方案购买较为合算。
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的方案,并计算出所需的钱数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x+3与y轴交于A点,与反比例函数y=
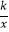 (x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).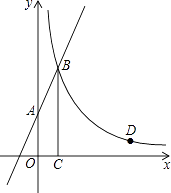
(1)求反比例函数的解析式;
(2)点D(a,1)是反比例函数y=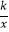 (x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
相关试题

