【题目】如图,长方形![]() 中,
中,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 匀速运动;点
匀速运动;点![]() 从点
从点![]() 出发,沿
出发,沿![]() 的路径匀速运动.两点同时出发,在
的路径匀速运动.两点同时出发,在![]() 点处首次相遇后,点
点处首次相遇后,点![]() 的运动速度每秒提高了
的运动速度每秒提高了![]() ,并沿
,并沿![]() 的路径匀速运动;点
的路径匀速运动;点![]() 保持速度不变,继续沿原路径匀速运动,某一时刻两点在长方形
保持速度不变,继续沿原路径匀速运动,某一时刻两点在长方形![]() 某一边上的
某一边上的![]() 点处第二次相遇.若点
点处第二次相遇.若点![]() 的速度为
的速度为![]() .
.
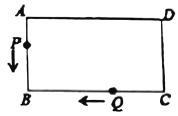
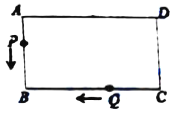
备用图
(1)点![]() 原来的速度为___________
原来的速度为___________![]() .
.
(2)![]() ,
,![]() 两点在
两点在![]() 点处首次相遇后,再经过___________秒后第二次在
点处首次相遇后,再经过___________秒后第二次在![]() 点相遇.
点相遇.
(3)![]() 点在___________边上.此时
点在___________边上.此时![]() ___________
___________![]() .
.
(4)在![]() 点相遇后
点相遇后![]() ,
,![]() 两点沿原来的方向继续前进.又经历了
两点沿原来的方向继续前进.又经历了![]() 次相遇后停止运动,请问此时两点停在长方形
次相遇后停止运动,请问此时两点停在长方形![]() 边上的什么位置?
边上的什么位置?
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;AD;
;AD; ![]() ;(4)Q点移动99次后与P点相遇在AD上,且距离A点
;(4)Q点移动99次后与P点相遇在AD上,且距离A点![]() 处.
处.
【解析】
(1)根据题意可得点![]() 原来的速度为
原来的速度为![]() 点的速度的两倍,故可求解;
点的速度的两倍,故可求解;
(2)设经过xs相遇,根据题意列出方程即可求解;
(3)由(2)可得到移动的路程,即可求出E点位置,再求出![]() ;
;
(4)根据每次相遇移动的时间相等,故求出Q点移动99次后的路程,即可得到终点位置.
(1)∵两点同时出发,在![]() 点处首次相遇后,
点处首次相遇后,![]() , 点
, 点![]() 的速度为
的速度为![]() .
.
∴点![]() 原来的速度为
原来的速度为![]() 点的速度的两倍,
点的速度的两倍,
故点![]() 原来的速度为
原来的速度为![]()
![]()
故答案为![]() ;
;
(2)设经过xs相遇,
依题意得![]()
解得x=![]() s
s
故答案为![]() ;
;
(3)依题意知Q点经过![]() 秒到达E点,
秒到达E点,
故经过的路程为![]() ×
×![]() =
=![]()
∵AB=4,
∴![]() -4=
-4=![]() <8
<8
E点在AD上,DE=8-![]() =
=![]()
![]()
![]() DE×CD=
DE×CD=![]() ×
×![]() ×4=
×4=![]()
故答案为:AD; ![]() ;
;
(4)∵每次相遇移动的时间为t=![]()
∴Q点移动99次后的路程为99×![]() ×
×![]() =
=![]()
![]() ÷24=
÷24=![]() =
=![]()
故Q点移动25圈,
又![]() =
=![]()
![]() -4=
-4=![]() <8
<8
∴Q点移动99次后与P点相遇在AD上,且距离A点![]() 处.
处.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校实行学案式教学,需印制若干份教学学案.印刷厂有,甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示.

(1)填空:甲种收费方式的函数关系式是__________,乙种收费方式的函数关系式是__________.
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一定数目的点或大小相同的圆在等距离的排列下可以形成一个等边三角形数阵.古希腊著名数学家毕达哥拉斯用数
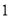 ,
,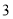 ,
,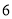 ,
,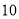 ,
,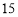 ,
,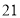 ……这些数量的(石子),都成功的排成了等边三角形数阵..
……这些数量的(石子),都成功的排成了等边三角形数阵..(问题提出)
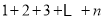 结果等于多少?
结果等于多少?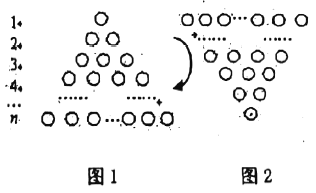
在图1所示的等边三角形数阵中,前
 行有
行有 个圆圈,前
个圆圈,前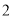 行有
行有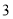 个圆圈,即
个圆圈,即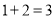 ,前
,前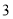 行有
行有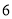 个圆圈,即
个圆圈,即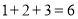 ,…,则前
,…,则前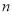 行所有圆圈个数总和为
行所有圆圈个数总和为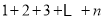
将图1旋转至图2,观察这两个三角形数阵中同一行圆圈个数(如第
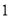 行的圆圈个数分别为
行的圆圈个数分别为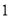 个,
个,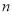 个),发现同一行圆圈个数之和均为___________个,由此可得两个图前
个),发现同一行圆圈个数之和均为___________个,由此可得两个图前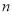 行圆圈个数总和为:
行圆圈个数总和为: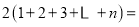 ___________,因此,
___________,因此,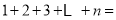 ___________.
___________.(问题延伸)
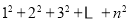 结果等于多少?
结果等于多少?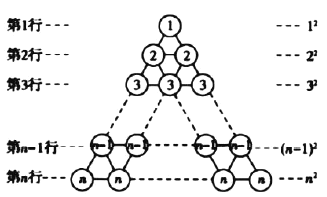
图3
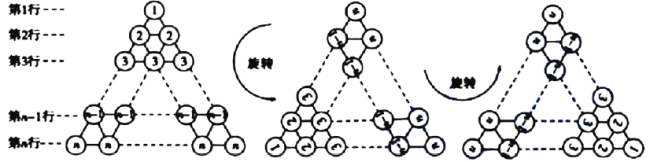
图4
在图3所示的等边三角形数阵中,第
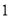 行圆圈中的数为
行圆圈中的数为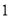 ,即
,即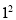 ,第
,第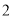 行两个圆圈中数字的和为
行两个圆圈中数字的和为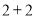 .即
.即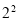 …,第
…,第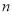 行
行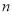 个圆圈中数字的和为
个圆圈中数字的和为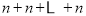 (共
(共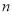 个).即
个).即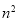 .这样,该三角形数阵中所有圆圈中数字的和为
.这样,该三角形数阵中所有圆圈中数字的和为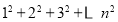 .
.将该三角形数阵经两次旋转可得如图4所示的三个三角形数阵,观察这三个三角形数阵中各行同一位置上圆圈中的数字(如第
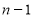 行的第一个圆圈中的数字分别为
行的第一个圆圈中的数字分别为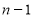 ,
,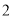 ,
,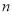 ),发现相同位置上三个圆圈中数字之和均为___________,由此可得,这三个三角形数阵所有圆圈中数字的总和为:
),发现相同位置上三个圆圈中数字之和均为___________,由此可得,这三个三角形数阵所有圆圈中数字的总和为: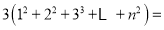 ___________,因此,
___________,因此,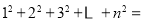 ___________.
___________.(规律应用)
根据以上发现,计算:
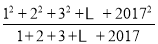 的结果为___________.
的结果为___________. -
科目: 来源: 题型:
查看答案和解析>>【题目】用火柴棒按下列方式搭建三角形:

三角形个数
1
2
3
4
…
火柴棒根数
3
5
7
9
…
(1)当三角形的个数为n时,火柴棒的根数是多少?
(2)求当n=100时,有多少根火柴棒?
(3)当火柴棒的根数为2017时,三角形的个数是多少?
-
科目: 来源: 题型:
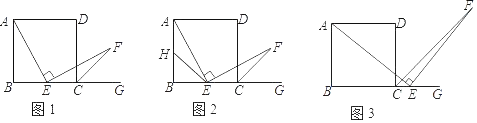
查看答案和解析>>【题目】如图1,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形ABCD的外角∠DCG的平分线CF于点F.
(1)如图2,取AB的中点H,连接HE,求证:AE=EF.
(2)如图3,若点E是BC的延长线上(除C点外)的任意一点,其他条件不变结论“AE=EF”仍然成立吗?如果正确,写出证明过程:如果不正确,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若∠BEC=30°,求证:以BC,BE,AC边的三角形为直角三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家想要从某场购买洗衣机和烘干机各一台,现在分别从
 两个品牌中各选中一款洗衣机和一款烘干机,它们的单价如表1所示.目前该商场有促销活动,促销方案如表2所示.
两个品牌中各选中一款洗衣机和一款烘干机,它们的单价如表1所示.目前该商场有促销活动,促销方案如表2所示.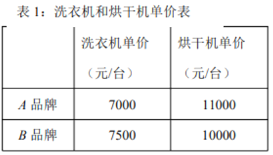
表2:商场促销方案
1. 所有商品均享受8折优惠.
2. 所有洗衣机均可享受节能减排补
贴,补贴标准为:在折后价的基础t.
再减免13%。
3.若同时购买同品牌洗 衣机和烘干
机,额外可享受“满两件减400元"
则选择_____品种的洗衣机和_____品种的烘干机支付总费用最低,支付总费用最低为___________元.
相关试题

