【题目】如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC,BC边上,C,D两点不重合,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )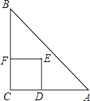
A.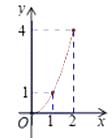
B.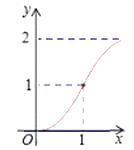
C.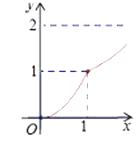
D.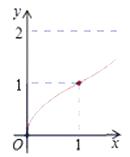
参考答案:
【答案】B
【解析】当0<x≤1时,y=x2 ,
当1<x≤2时,ED交AB于M,EF交AB于N,如图,
CD=x,则AD=2-x,
∵Rt△ABC中,AC=BC=2,
∴△ADM为等腰直角三角形,
∴DM=2-x,
∴EM=x-(2-x)=2x-2,
∴S△ENM= ![]() (2x-2)2=2(x-1)2 ,
(2x-2)2=2(x-1)2 ,
∴y=x2-2(x-1)2=-x2+4x-2=-(x-2)2+2,
∴y= ![]() .
.
故答案为:B.
分类讨论:当0<x≤1时,根据正方形的面积公式得到y=x2;当1<x≤2时,ED交AB于M,EF交AB于N,利用重叠的面积等于正方形的面积减去等腰直角三角形MNE的面积得到y=x2-2(x-1)2 , 配方得到y=-(x-2)2+2,然后根据二次函数的性质对各选项进行判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)观察推理:如图 1,△ABC 中,∠ACB=90°,AC=BC,直线 L 过点C,点 A,B 在直线 L 同侧,BD⊥L, AE⊥L,垂足分别为D,E
求证:△AEC≌△CDB
(2)类比探究:如图 2,Rt△ABC 中,∠ACB=90°,AC=4,将斜边 AB 绕点 A 逆时针旋转 90°至 AB’, 连接B’C,求△AB’C 的面积
(3)拓展提升:如图 3,等边△EBC 中,EC=BC=3cm,点 O 在 BC 上且 OC=2cm,动点 P 从点 E 沿射线EC 以 1cm/s 速度运动,连接 OP,将线段 OP 绕点O 逆时针旋转 120°得到线段 OF,设点 P 运动的时间为t 秒。
当t= 秒时,OF∥ED


若要使点F 恰好落在射线EB 上,求点P 运动的时间t
-
科目: 来源: 题型:
查看答案和解析>>【题目】要在宽为22米的九州大道AB两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )
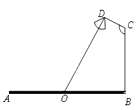
A. 米
米
B. 米
米
C. 米
米
D. 米
米 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在半径为6cm的⊙O中,点A是劣弧
 的中点,点D是优弧
的中点,点D是优弧  上一点,且∠D=30下列四个结论:①OA⊥BC;②BC=
上一点,且∠D=30下列四个结论:①OA⊥BC;②BC=  cm;③cos∠AOB=
cm;③cos∠AOB=  ;④四边形ABOC是菱形.其中正确结论的序号是( )
;④四边形ABOC是菱形.其中正确结论的序号是( )
A.①③
B.①②③④
C.①②④
D.②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】2019年是大家公认的
 商用元年.移动通讯行业人员想了解
商用元年.移动通讯行业人员想了解 手机的使用情况,在某高校随机对500位大学生进行了问卷调查.下列说法正确的是( )
手机的使用情况,在某高校随机对500位大学生进行了问卷调查.下列说法正确的是( )A.该调查方式是普查
B.该调查中的个体是每一位大学生
C.该调查中的样本是被随机调查的500位大学生
 手机的使用情况
手机的使用情况D.该调査中的样本容量是500位大学生
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车同时从A地出发,各自都以自己的速度匀速向B地行驶,甲车先到B地,停车1小时后按原速匀速返回,直到两车相遇.已知,乙车的速度是60千米/时,如图是两车之间的距离y(千米)与乙车行驶的时间x(小时)之间的函数图象,则下列说法不正确的是( )

A.A、B两地之间的距离是450千米
B.乙车从出发到与甲车返回时相遇所用的时间是6.6小时
C.甲车的速度是80千米/时
D.点M的坐标是(6,90)
-
科目: 来源: 题型:
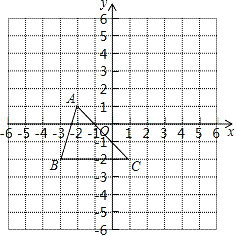
查看答案和解析>>【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1.
(1)在图中画出△A1B1C1;
(2)点A1,B1,C1的坐标分别为 、 、 ;
(3)若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.
相关试题

