搜索
【题目】要在宽为22米的九州大道AB两边安装路灯，路灯的灯臂CD长2米，且与灯柱BC成120°角，路灯采用圆锥形灯罩，灯罩的轴线DO与灯臂CD垂直，当灯罩的轴线DO通过公路路面的中心线时照明效果最佳，此时，路灯的灯柱BC高度应该设计为（ ）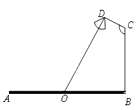
A.
米
B.
米
C.
米
D.
米
参考答案：
【答案】B
【解析】如图，延长OD，BC交于点P．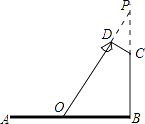
∵∠ODC=∠B=90°，∠P=30°，OB=11米，CD=2米，
∴在直角△CPD中，DP=DCcot30°=2 
m，PC=CD÷（sin30°）=4米，
∵∠P=∠P，∠PDC=∠B=90°，
∴△PDC∽△PBO，
∴ 
，
∴PB= 
米，
∴BC=PB-PC= 
米．
故答案为：B．
出现有直角的四边形时，应构造相应的直角三角形，利用相似求得PB、PC，再相减即可求得BC长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，等腰直角△ABC中，AB=AC=8，以AB为直径的半圆O交斜边BC于D，则阴影部分的面积为（结果保留π）（ ）
A.
B.
C.
D.16 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图①所示，已知，BC∥OA，∠B=∠A=100°，试解答下列问题：
（1）试说明：OB∥AC；
（2）如图②，若点E．F在BC上，且∠FOC=∠AOC，OE平分∠BOF.试求∠EOC的度数；
（3）在（2）小题的条件下，若左右平行移动AC，如图③，那么∠OCB：∠OFB的比值是否随之发生变化？若变化，试说明理由；若不变，求出这个比值.
（4）在（3）小题的条件下，当∠OEB=∠OCA时，试求∠OCA的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】(1)观察推理：如图 1，△ABC 中，∠ACB=90°，AC=BC,直线 L 过点C，点 A,B 在直线 L 同侧，BD⊥L， AE⊥L，垂足分别为D,E
求证:△AEC≌△CDB
（2）类比探究：如图 2，Rt△ABC 中，∠ACB=90°，AC=4，将斜边 AB 绕点 A 逆时针旋转 90°至 AB’, 连接B’C，求△AB’C 的面积
（3）拓展提升：如图 3，等边△EBC 中，EC=BC=3cm，点 O 在 BC 上且 OC=2cm，动点 P 从点 E 沿射线EC 以 1cm/s 速度运动，连接 OP,将线段 OP 绕点O 逆时针旋转 120°得到线段 OF，设点 P 运动的时间为t 秒。
当t= 秒时，OF∥ED
若要使点F 恰好落在射线EB 上，求点P 运动的时间t
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在半径为6cm的⊙O中，点A是劣弧
的中点，点D是优弧 上一点，且∠D=30下列四个结论：①OA⊥BC；②BC= 
cm；③cos∠AOB= 
；④四边形ABOC是菱形.其中正确结论的序号是（ ）
A.①③
B.①②③④
C.①②④
D.②③④ -
科目： 来源： 题型：
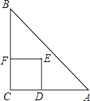
查看答案和解析>>【题目】如图，Rt△ABC中，AC=BC=2，正方形CDEF的顶点D、F分别在AC，BC边上，C，D两点不重合，设CD的长度为x，△ABC与正方形CDEF重叠部分的面积为y，则下列图象中能表示y与x之间的函数关系的是（ ）
A.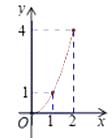
B.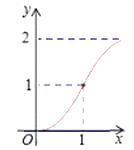
C.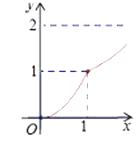
D.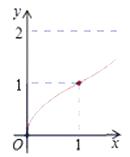
-
科目： 来源： 题型：
查看答案和解析>>【题目】2019年是大家公认的
商用元年．移动通讯行业人员想了解手机的使用情况，在某高校随机对500位大学生进行了问卷调查．下列说法正确的是（ ）A.该调查方式是普查
B.该调查中的个体是每一位大学生
C.该调查中的样本是被随机调查的500位大学生
手机的使用情况D.该调査中的样本容量是500位大学生
相关试题
