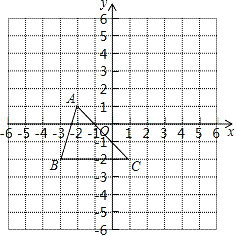
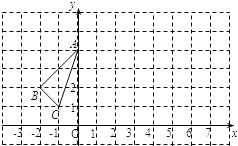
【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1.
(1)在图中画出△A1B1C1;
(2)点A1,B1,C1的坐标分别为 、 、 ;
(3)若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.
参考答案:
【答案】(1)画图见解析;(2)(0,4),(﹣1,1),(3,1);(3)点P的坐标为(0,1)或(0,﹣5).
【解析】试题分析:(1)按要求进行平移即可;
(2)根据平移的图形,观察即可得点的坐标;
(3)两三角形面积相等,则相对于BC边,两三角形高相等,设P(0,y),由三角形的面积公式得|y-(-2)|=3 ,从而可得点P的坐标.
试题解析:(1)如图所示:
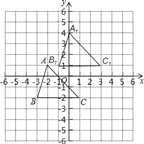
(2)(0,4),(﹣1,1),(3,1);
(3)设P(0,y),由三角形的面积公式得:S△PBC=![]() ×4×|y-(-2)|=
×4×|y-(-2)|=![]() ×4×3=6,
×4×3=6,
解得|y-(-2)|=3,
∴点P的坐标为(0,1)或(0,﹣5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前节能灯在城市已基本普及,为响应号召,某商场计划用3800元购进甲,乙两种节能灯共120只,这两种节能灯的进价、售价如下表:
进价(元/只)
售价(元/只)
甲型
25
30
乙型
45
60
(1)求甲、乙两种节能灯各进多少只?
(2)全部售完120只节能灯后,该商场获利多少元?
-
科目: 来源: 题型:
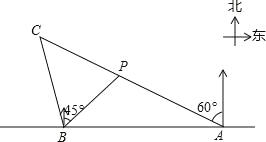
查看答案和解析>>【题目】如图,在笔直的海岸线l上有A、B两个观测站,A在B的正东方向,AB=(
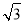 +1)km,小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°方向.
+1)km,小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°方向.(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到达点C处,此时,从B测得小船在北偏西15°的方向,求点C与点B之间的距离.(友情提示:结果都保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C1和△A2B2C2,它们是否关于某条直线对称?若是,请在图上画出这条对称轴.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a3﹣a2=a B. a2a3=a6 C. a6÷a2=a3 D. (a2)3=a6
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a2+a2=a4B. 3(a﹣b)=3a﹣b
C. (﹣b2)3=﹣b5D. a2a2=a4
-
科目: 来源: 题型:
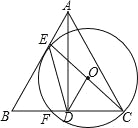
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,E为边AB上一点,ED=CD,以CE为直径作⊙O,交BC于点F.
(1)求证:AB与⊙O相切;
(2)若DF=1,DC=3,求AE的长.
相关试题

