【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() ,
,![]() ,将线段
,将线段![]() 平移至
平移至![]() ,点
,点![]() 在
在![]() 轴正半轴上(不与点
轴正半轴上(不与点![]() 重合),连接
重合),连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
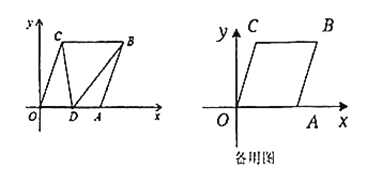
(1)写出点![]() 的坐标;
的坐标;
(2)当![]() 的面积是
的面积是![]() 的面积的3倍时,求点
的面积的3倍时,求点![]() 的坐标;
的坐标;
(3)设![]() ,
,![]() ,
,![]() ,判断
,判断![]() 、
、![]() 、
、![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
参考答案:
【答案】(1)![]() ;(2)①若点
;(2)①若点![]() 在线段
在线段![]() 上,
上,![]() ;②若点
;②若点![]() 在线段
在线段![]() 延长线上,
延长线上,![]() ;(3)①若点
;(3)①若点![]() 在线段
在线段![]() 上,
上,![]() ;②若点
;②若点![]() 在线段
在线段![]() 延长线上,
延长线上,![]() ,见解析.
,见解析.
【解析】
(1)过C点作CF⊥y轴与点F,过B点作BE⊥x轴与点E,根据平移的性质可得OA=BC,OF=BE,进而得到C点坐标;
(2)分点![]() 在线段
在线段![]() 上和点
上和点![]() 在线段
在线段![]() 延长线上两种情况进行讨论,
延长线上两种情况进行讨论,![]() 与
与![]() 的高都是一样的,所以只要底边符合条件即可;
的高都是一样的,所以只要底边符合条件即可;
(3)分点![]() 在线段
在线段![]() 上和点
上和点![]() 在线段
在线段![]() 延长线上两种情况进行讨论,过点
延长线上两种情况进行讨论,过点![]() 作
作![]() ,利用平行线的性质进行证明即可.
,利用平行线的性质进行证明即可.
解:(1)如图1,过C点作CF⊥y轴与点F,过B点作BE⊥x轴与点E,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
(2)设![]() ,
,
①若点![]() 在线段
在线段![]() 上,
上,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
②若点![]() 在线段
在线段![]() 延长线上,
延长线上,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
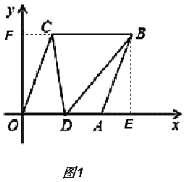
(3)如图2、3,过点![]() 作
作![]() ,
,
由平移的性质知![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() (两直线平行,内错角相等),
(两直线平行,内错角相等),
①若点![]() 在线段
在线段![]() 上,(图2)
上,(图2)
![]() ,
,
即![]() ;
;
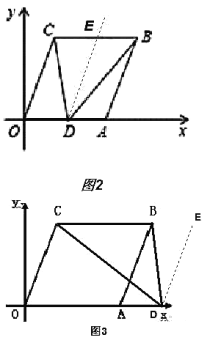
②若点![]() 在线段
在线段![]() 延长线上,(图3)
延长线上,(图3)
![]() ,
,
即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系第一象限中,已知点A坐标为(1,0),点D坐标为(1,3),点G坐标为(1,1),动点E从点G出发,以每秒1个单位长度的速度匀速向点D方向运动,与此同时,x轴上动点B从点A出发,以相同的速度向右运动,两动点运动时间为t(0<t<2),以AD、AB分别为边作矩形ABCD,过点E作双曲线交线段BC于点F,作CD中点M,连接BE、EF、EM、FM.
(1)当t=1时,求点F的坐标.
(2)若BE平分∠AEF,则t的值为多少?
(3)若∠EMF为直角,则t的值为多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点E、F分别在边AB和CD上,下列条件不能判定四边形DEBF一定是平行四边形的是( )

A.AE=CFB.DE=BFC.∠ADE=∠CBFD.∠AED=∠CFB
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E,F是对角线AC上的两点,且AE=CF.下列结论:①BE=DF;②BE∥DF;③AB=DE;④四边形EBFD为平行四边形;⑤S△ADE=S△ABE;⑥AF=CE.其中正确的个数是( )

A. 3个 B. 4个 C. 5个 D. 6个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC,BD相交于点O,点E在AB上,且BE=BO,则∠EOA=___________°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】苏州太湖养殖场计划养殖蟹和贝类产品,这两个品种的种苗的总投放量只有50吨,根据经验测算,这两个品种的种苗每投放一吨的先期投资,养殖期间的投资以及产值如下表(单位:万元/吨)
品种
先期投资
养殖期间投资
产值
贝类产品
0.9
0.3
0.33
蟹产品
0.4
1
2
养殖场受经济条件的影响,先期投资不超过36万元,养殖期间的投资不超过29万元,设贝类的种苗投放量为x吨,
(1)求x的取值范围;
(2)设这两个品种产出后的总产值为y(万元),试写出y与x之间的函数关系式,并求出当x等于多少时,y有最大值?最大值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下表回答问题:
x
16
16.1
16.2
16.3
16.4
16.5
16.6
16.7
16.8
x2
256
259.21
262.44
265.69
268.96
272.25
175.56
278.89
282.24
(1)272.25的平方根是
(2)
 = ,
= ,  = ,
= , 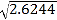 =
= (3)设
 的整数部分为a,求﹣4a的立方根.
的整数部分为a,求﹣4a的立方根.
相关试题

