【题目】在平面直角坐标系中,若要把一条直线平移到某个位置,经常可通过方式一:上(下)平移,或者方式二:左(右)平移的其中一种达到目的.现有直线![]() 交
交![]() 轴于点
轴于点![]() ,若把直线
,若把直线![]() 向右平移8个单位长度得到直线
向右平移8个单位长度得到直线![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求直线![]() 的解析式,并说明直线
的解析式,并说明直线![]() 若按方式一是如何平移到直线
若按方式一是如何平移到直线![]() 的位置;
的位置;
(2)若直线![]() 上的一点
上的一点![]() ,点
,点![]() 按方式一平移后在直线
按方式一平移后在直线![]() 上的对应点记为点
上的对应点记为点![]() .
.
①若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示) ;
的式子表示) ;
②当![]() 时,试证明直线
时,试证明直线![]() 必将四边形
必将四边形![]() 的面积二等分.
的面积二等分.

参考答案:
【答案】(1)![]() ,向上平移4个单位;(2)①点
,向上平移4个单位;(2)①点![]() 的坐标为
的坐标为![]() ;②证明见解析
;②证明见解析
【解析】
(1)根据直线平行k相等,可求直线![]() 的解析式,根据两直线与x轴交点坐标可确定按方式一是如何平移到直线
的解析式,根据两直线与x轴交点坐标可确定按方式一是如何平移到直线![]() 的;
的;
(2)①根据B在直线![]() 上可得
上可得![]() ,由B的对应点为C,可得点C
,由B的对应点为C,可得点C![]() ,且BC∥y轴,由中点坐标公式可得中点坐标,根据线段垂直平分线的性质得点P在BC的垂直平分线上,即点P的纵坐标和BC中点的纵坐村都是
,且BC∥y轴,由中点坐标公式可得中点坐标,根据线段垂直平分线的性质得点P在BC的垂直平分线上,即点P的纵坐标和BC中点的纵坐村都是![]() ,设点P的横坐标为
,设点P的横坐标为![]() ,代入可得结论;
,代入可得结论;
②证明四边形ABCD是平行四边形,连接BD、AC,交点记为点E,确定E![]() ,则过点E的直线把平行四边形ABCD的面积二等分,再证明直线直线
,则过点E的直线把平行四边形ABCD的面积二等分,再证明直线直线![]() 必过E点,可得结论.
必过E点,可得结论.
解:(1)![]() ,
,
当![]() 时,
时,![]() ,
,
∴直线![]() 与
与![]() 轴交点坐标为
轴交点坐标为![]() ,
,
按方式二平移后的对应点为![]() ,且在直线
,且在直线![]() 上,
上,
设直线![]() 的解析式为
的解析式为![]()
∴![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
![]() ,
,
∴直线![]() 若按方式一向上平移4个单位得到直线
若按方式一向上平移4个单位得到直线![]() ;
;
(2)①如图1,∵点![]() 在直线
在直线![]() 上,
上,
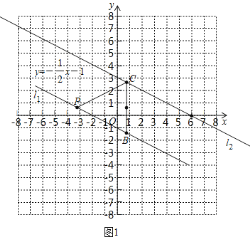
![]() ,
,
∴点![]() ,
,
由(1)得,点![]() ,且
,且![]() 轴,
轴,
∴![]() 的中点坐标为
的中点坐标为![]() ,
,
![]()
∴点![]() 在
在![]() 的垂直平分线上,
的垂直平分线上,
又∵![]() 轴,
轴,
∴点![]() 的纵坐标为
的纵坐标为![]() ,
,
设点![]() 的横坐标为
的横坐标为![]() ,
,
![]() ,
,
![]()
∴点![]() 的坐标为
的坐标为![]() ;
;
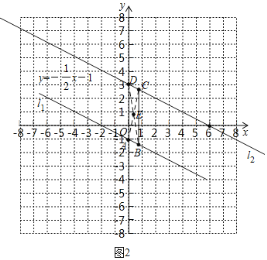
②如图2,根据题意得:![]() ,
,![]() ,
,![]()
![]() ,
,
由平移可知![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
连接四边形![]() 的对角线,交点记为点
的对角线,交点记为点![]() ,则
,则![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]()
![]() 过点
过点![]() 的直线把平行四边形
的直线把平行四边形![]() 的面积二等分,
的面积二等分,
把![]() 代入
代入![]() 中,得
中,得![]() ,
,
即当![]() 时,直线
时,直线![]() 必过
必过![]() 点,
点,
直线![]() 必将四边形
必将四边形![]() 的面积二等分.
的面积二等分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图1,在
 中,
中, ,
, ,
, ,点
,点 分别是
分别是 的中点,分别延长
的中点,分别延长 到点
到点 ,使得
,使得 ,连接
,连接 .
.(1)求证:四边形
 是矩形;
是矩形;(2)如图2,连接
 ,若
,若 平分
平分 .
.①求
 的长;
的长;②如图3,连接
 ,分别交
,分别交 于点
于点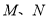 .求证:
.求证: 是等腰三角形.
是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级学生小聪和小明完成了数学实验《钟面上的数学》之后,自制了一个模拟钟面,如图所示,O为模拟钟面圆心,M、O、N在一条直线上,指针OA、OB分别从OM、ON出发绕点O转动,OA运动速度为每秒15°,OB运动速度为每秒5°,当一根指针与起始位置重合时,运动停止,设转动的时间为t秒,请你试着解决他们提出的下列问题:
(1)若OA顺时针转动,OB逆时针转动,t= 秒时,OA与OB第一次重合;
(2)若它们同时顺时针转动,
①当 t=2秒时,∠AOB= °;
②当t为何值时,OA与OB第一次重合?
③当t为何值时,∠AOB=30°?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.

(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行.本届论坛期间,中国同30多个国家签署经贸合作协议.某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区.已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件? -
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。

根据以上信息,解答下列问题:
(1)设租车时间为 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为  元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为  元,分别求出
元,分别求出  ,
,  关于
关于  的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知直线PQ∥MN,点A、B分别在直线MN、PQ上,射线AM绕点A以5°/秒的速度按顺时针开始旋转,旋转至与AN(或AM)重合后便立即回转,射线BQ绕点B以2°/秒的速度按顺时针开始旋转,旋转至与BP重合后便停止转动,旋转后的射线分别记为AM'和BQ'.
(1)若射线BQ先转动30秒,射线AM才开始转动,在射线AM第一次到达AN之前,射线AM转动几秒后AM'∥BQ';
(2)若射线AM,BQ同时转动t秒,在射线BQ停止转动之前,记射线AM'与BQ'交于点H,若∠AHB=90°,求t的值;
(3)射线AM,BQ同时转动,在射线AM第一次到达AN之前,记射线AM'与BQ'交于点K,过K作KC⊥AK交PQ于点C,如图2,若∠BAN=30°,则在旋转过程中,∠BAK与∠BKC有何数量关系?并说明理由.

相关试题

