【题目】七年级学生小聪和小明完成了数学实验《钟面上的数学》之后,自制了一个模拟钟面,如图所示,O为模拟钟面圆心,M、O、N在一条直线上,指针OA、OB分别从OM、ON出发绕点O转动,OA运动速度为每秒15°,OB运动速度为每秒5°,当一根指针与起始位置重合时,运动停止,设转动的时间为t秒,请你试着解决他们提出的下列问题:
(1)若OA顺时针转动,OB逆时针转动,t= 秒时,OA与OB第一次重合;
(2)若它们同时顺时针转动,
①当 t=2秒时,∠AOB= °;
②当t为何值时,OA与OB第一次重合?
③当t为何值时,∠AOB=30°?

参考答案:
【答案】(1)9(2)①160;②18;③t=15或21
【解析】
(1)根据题意可知两针相遇,可知两针总共转出了180°可列方程求解;
(2)①根据所给的时间求出各自转出的角度,然后可列方程求解;
②根据它们的重合可知它们之差为180度列方程求解;
③可根据同向旋转和相向转动的差为30°列方程求解.
(1)t=9秒
(2)①当 t=2秒时,∠AOB=160°;
②设t秒后第一次重合.
15t﹣5t=180,
t=18.
∴t=18秒时,第一次重合.
③设t秒后∠AOB=30°,
由题意15t﹣5t=180-30或15t﹣5t=180+30,
∴t=15或21.
∴t=15或21秒时,∠AOB=30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列方程,属于一元一次方程的有( )
①x﹣2=
 ;②0.5x=1;③
;②0.5x=1;③ =8x﹣1;④x2﹣4x=8;⑤x=0;⑥x+2y=0.
=8x﹣1;④x2﹣4x=8;⑤x=0;⑥x+2y=0.A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学习小组在学习了函数及函数图象的知识后,想利用此知识来探究周长一定的矩形其边长分别为多少时面积最大. 请将他们的探究过程补充完整.
(1)列函数表达式:若矩形的周长为8,设矩形的一边长为x,面积为y,则有y=____________;
(2)上述函数表达式中,自变量x的取值范围是____________;
(3)列表:
x
…
0.5
1
1.5
2
2.5
3
3.5
…
y
…
1.75
3
3.75
4
3.75
3
m
…
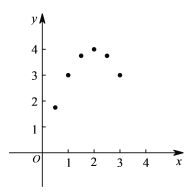
写出m=____________;
(4)画图:在平面直角坐标系中已描出了上表中部分各对应值为坐标的点,请你画出该函数的图象;
(5)结合图象可得,x=____________时,矩形的面积最大;写出该函数的其它性质(一条即可):____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们,足球是世界上第一大运动,你热爱足球运动吗?已知在足球比赛中,胜一场得3分,平一场得1分,负一场得0分,一队共踢了30场比赛,负了9场,共得47分,那么这个队胜了( )
A. 10场 B. 11场 C. 12场 D. 13场
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E是边BC的中点,直线EF交正方形外角的平分线于点F,交DC于点G,且AE⊥EF.

(1)当AB=2时,求GC的长;
(2)求证:AE=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l分别交x轴、y轴于A、B两点,AB=5,OA:OB =3:4.
(1)求直线l的表达式;
(2)点P是
 轴上的点,点Q是第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q点的坐标.
轴上的点,点Q是第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q点的坐标.
-
科目: 来源: 题型:
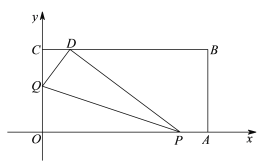
查看答案和解析>>【题目】如图,将一矩形纸片OABC放在平面直角坐标系中,
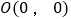 ,
,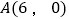 ,
, .动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动
.动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动 秒时,动点P从点A出发以相同的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).
秒时,动点P从点A出发以相同的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).(1)OP =____________, OQ =____________;(用含t的代数式表示)
(2)当
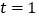 时,将△OPQ沿PQ翻折,点O恰好落在CB边上的点D处.
时,将△OPQ沿PQ翻折,点O恰好落在CB边上的点D处.①求点D的坐标;
②如果直线y = kx + b与直线AD平行,那么当直线y = kx + b与四边形PABD有交点时,求b 的取值范围.
相关试题

