【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
根据以上信息,解答下列问题:
(1)设租车时间为 ![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为 ![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为 ![]() 元,分别求出
元,分别求出 ![]() ,
, ![]() 关于
关于 ![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
参考答案:
【答案】
(1)
解:由题可知:y1=k1x+80,
∵图像过点(1,95),
∴95=k1+80,
∴k1=15,
∴y1=15x+80(x≥0)
由题可知:y2=30x(x≥0).
(2)
解:当y1=y2时,解得x=![]() ,
,
当y1>y2时,解得x>![]() ,
,
当y1<y2时,解得x<![]() ,
,
∴当租车时间为![]() 小时,选择甲乙公司一样合算;当租车时间小于
小时,选择甲乙公司一样合算;当租车时间小于![]() 小时,选择乙公司合算;当租车时间大于
小时,选择乙公司合算;当租车时间大于![]() 小时,选择甲公司合算。
小时,选择甲公司合算。
【解析】(1)根据题意与图像,列出y1与y2关于x的函数表达式。
(2)比较y1与y2大小即可知道哪种方案合算。
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
∵
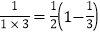 ,
,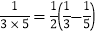 ,
,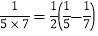 ,……
,……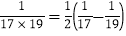 ,
,∴
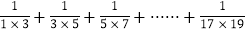
=
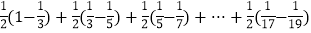
=
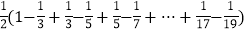 =
=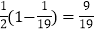 .
.解答下列问题:
(1)在和式
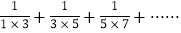 中,第6项为______,第n项是__________.
中,第6项为______,第n项是__________.(2)上述求和的想法是通过逆用________法则,将和式中的各分数转化为两个数之差,使得除首末两项外的中间各项可以_______,从而达到求和的目的.
(3)受此启发,请你解下面的方程:
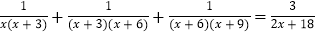 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,等边△OAB的顶点A在x轴的负半轴上,点B(a,b)在第二象限内,且a,b满足
 .点P是y轴上的一个动点,以PA为边作等边△PAC,直线BC交x轴于点M,交y轴于点D.
.点P是y轴上的一个动点,以PA为边作等边△PAC,直线BC交x轴于点M,交y轴于点D.(1)求点A的坐标;
(2)如图2,当点P在y轴正半轴上时,求点M的坐标;
(3)如图3,当点P在y轴负半轴上时,求出OP,CD,AD满足的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
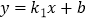 (
( 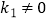 )与反比例函数
)与反比例函数 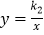 (
( 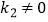 )的图象交于点
)的图象交于点 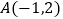 ,
, 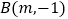 .
.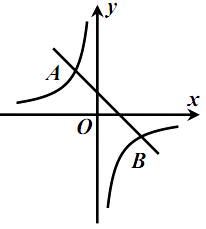
(1)求这两个函数的表达式;
(2)在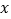 轴上是否存在点
轴上是否存在点 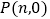
 ,使
,使 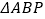 为等腰三角形?若存在,求
为等腰三角形?若存在,求 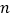 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DE∥BC, AB∥CD,E为AB的中点,∠A=∠B.下列结论:①CD=AE;②AC=DE;③AC平分∠BCD;④O点是DE的中点;⑤AC=AB.其中正确的是( )
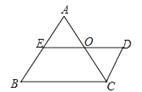
A. ①②④ B. ①③⑤ C. ②③④ D. ②④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )

A. 105° B. 110° C. 100° D. 120°
相关试题

