【题目】如图1,已知直线PQ∥MN,点A、B分别在直线MN、PQ上,射线AM绕点A以5°/秒的速度按顺时针开始旋转,旋转至与AN(或AM)重合后便立即回转,射线BQ绕点B以2°/秒的速度按顺时针开始旋转,旋转至与BP重合后便停止转动,旋转后的射线分别记为AM'和BQ'.
(1)若射线BQ先转动30秒,射线AM才开始转动,在射线AM第一次到达AN之前,射线AM转动几秒后AM'∥BQ';
(2)若射线AM,BQ同时转动t秒,在射线BQ停止转动之前,记射线AM'与BQ'交于点H,若∠AHB=90°,求t的值;
(3)射线AM,BQ同时转动,在射线AM第一次到达AN之前,记射线AM'与BQ'交于点K,过K作KC⊥AK交PQ于点C,如图2,若∠BAN=30°,则在旋转过程中,∠BAK与∠BKC有何数量关系?并说明理由.

参考答案:
【答案】(1)t=10s时,BQ′∥AM′;(2)满足条件的t的值为30秒或90秒.(3)![]()
【解析】
(1)当∠MAM′=∠QBQ′时,BQ′∥AM′,延长构建方程即可解决问题;
(2)根据点Q的运动时间t=90秒,分三种情形分别构建方程求解即可;
(3)如图3中,设∠KAB=x,∠BKC=y.设直线CK交MN于G.利用平行线的性质,构建方程组确定x与y之间的关系即可.
(1)由题意当5t=30+2t时,BQ′∥AM′,
∴t=10s时,BQ′∥AM′.
(2)∵点Q的运动时间t=![]() =90(秒),
=90(秒),
分三种情形:①射线AM第一次到达AN之前:如图1中,

当∠NAM′+∠QBQ′=90°时,∠AHB=90°,
则有2t+180°﹣5t=90°,
解得t=30(秒),
②射线AM返回途中:如图2中,

当∠MAM′+∠PBQ′=90°时,∠AHB=90°,
则有180°﹣2t+180°﹣(5t﹣180°)=90°,
解得t=![]() (秒)(不合题意舍弃),
(秒)(不合题意舍弃),
③射线AM第二次到达AN之前,如图2中,
当∠MAM′+∠PBQ′=90°时,∠AHB=90°,
则有180°﹣2t+(5t﹣360°)=90°,
解得t=90(秒),
综上所述,满足条件的t的值为30秒或90秒.
(3)如图3中,设∠KAB=x,∠BKC=y.设直线CK交MN于G.

∵AK⊥KC,
∴∠AKG=90°,
∴∠KAG+∠AGK=90°,
∵PQ∥MN,
∴∠AGK=∠QCK,
∴180°﹣5t+2t+y=90°,
∴t=30°﹣![]() y,
y,
∵x=30°﹣(180°﹣5t),
∴x=5t﹣150°,
∴x=5(30°﹣![]() y)﹣150°,
y)﹣150°,
∴x=![]() y,
y,
∴∠KAB=![]() ∠BKC.
∠BKC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,若要把一条直线平移到某个位置,经常可通过方式一:上(下)平移,或者方式二:左(右)平移的其中一种达到目的.现有直线
 交
交 轴于点
轴于点 ,若把直线
,若把直线 向右平移8个单位长度得到直线
向右平移8个单位长度得到直线 ,直线
,直线 交
交 轴于点
轴于点 .
.(1)求直线
 的解析式,并说明直线
的解析式,并说明直线 若按方式一是如何平移到直线
若按方式一是如何平移到直线 的位置;
的位置;(2)若直线
 上的一点
上的一点 ,点
,点 按方式一平移后在直线
按方式一平移后在直线 上的对应点记为点
上的对应点记为点 .
.①若点
 在直线
在直线 上,且
上,且 ,求点
,求点 的坐标(用含
的坐标(用含 的式子表示) ;
的式子表示) ;②当
 时,试证明直线
时,试证明直线 必将四边形
必将四边形 的面积二等分.
的面积二等分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行.本届论坛期间,中国同30多个国家签署经贸合作协议.某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区.已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件? -
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。

根据以上信息,解答下列问题:
(1)设租车时间为 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为  元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为  元,分别求出
元,分别求出  ,
,  关于
关于  的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要在平行四边形
 内作一个菱形.甲,乙两位同学的作法分别如下:
内作一个菱形.甲,乙两位同学的作法分别如下:
对于甲乙两人的作法,可判断( )
A.甲正确,乙错误B.甲错误,乙正确C.甲,乙均正确D.甲、乙均错误
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程(k-2)x2-4x+2=0有两个不相等的实数根.
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2-4x+k=0与x2+mx-1=0有一个相同的根,求此时m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于三个数a,b,c,M
 表示a,b,c这三个数的平均数,min
表示a,b,c这三个数的平均数,min 表示a,b,c这三个数中最小的数,如:
表示a,b,c这三个数中最小的数,如: M
 ,min
,min =-1;
=-1;M
 ,min
,min =
= ;
;解决下列问题:
(1) 填空:min{ a, a-1, a+2 }=______________;
(2) 若min
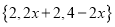 =2,则x的取值范围是______________;
=2,则x的取值范围是______________;(3) ①若M
 =min
=min ,那么x=______________;
,那么x=______________;②根据①,你发现结论“若M
 =min
=min ,则______________;(填a,b,c的大小关系);
,则______________;(填a,b,c的大小关系);③运用②解决问题:(写出求解的过程)
若M
 =min
=min ,
,求x+y 的值.
相关试题

