【题目】如图,四边形ABCD中,AB∥CD,AB⊥BC,AB=BC,AB>CD,AE⊥BD于E交BC于F.

(1)若AB=2CD;
①求证:BC=2BF;
②连CE,若DE=6,CE=![]() ,求EF的长;
,求EF的长;
(2)若AB=6,则CE的最小值为______.
参考答案:
【答案】(1)①见解析;②EF=2;(2) ![]() .
.
【解析】
(1)①证明△ABF≌△BCD(ASA),得出BF=CD,由已知AB=2CD,AB=BC,即可得出BC=2BF;
②设EF=x,证明△BEF∽△BCD,得出![]() ,用x依次表示出BE、BF、BC、CD、BD,然后根据6+BE=BD列出方程,解方程即可;
,用x依次表示出BE、BF、BC、CD、BD,然后根据6+BE=BD列出方程,解方程即可;
(2)取AB的中点O,连接OE,由直角三角形斜边上的中线性质得出OE= ![]() AB=3,当O、E、C三点共线时,OE+CE最短,此时CE最短.由勾股定理得出
AB=3,当O、E、C三点共线时,OE+CE最短,此时CE最短.由勾股定理得出![]() ,即可得出答案.
,即可得出答案.
(1)①证明:∵AB∥CD,AB⊥BC,
∴BC⊥CD,∠ABF=90°,∠BAF+∠BFE=90°,
∴∠BCD=90°,
∵AE⊥BD,
∴∠BEF=90°,
∴∠BFE+∠CBD=90°,
∴∠BAF=∠CBD,
在△ABF和△BCD中,
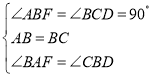 ,
,
∴△ABF≌△BCD(ASA),
∴BF=CD,
∵AB=2CD,AB=BC,
∴BC=2BF;
②解:∵∠BEF=∠BCD=90°,∠EBF=∠CBF,
∴△BEF∽△BCD,
![]() ,
,
∴![]() ,
,
∴设EF=x,则BE=2x,
∴BF= ![]() ,
,
∴BC= 2![]() ,CD=
,CD=![]() ,
,
∴BD= ![]() ,
,
∴6+2x=5x,
∴x=2,
∴EF=2;
(2)解:如图2所示:取AB的中点O,连接OE, 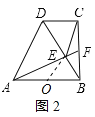
∵∠AEB=90°,AB=6,
∴OE=![]() AB=3,
AB=3,
当O、E、C三点共线时,OE+CE最短,此时CE最短,
∵BC=AB=6,∠ABC=90°,
∴OC= ![]()
∴CE的最小值=OC-OE= ![]()
故答案为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),对称轴l如图所示,则下列结论:①abc>0;②a﹣b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )
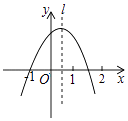
A.①③
B.②③
C.②④
D.②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2013次,点P依次落在点
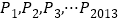 的位置,记
的位置,记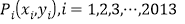 ,则P2013的横坐标x2013=______;如果
,则P2013的横坐标x2013=______;如果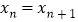 ,则
,则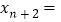 ______(请用含有n的式子表示).
______(请用含有n的式子表示).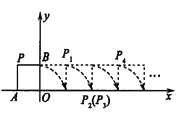
-
科目: 来源: 题型:
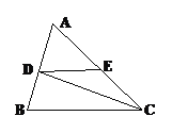
查看答案和解析>>【题目】如图,CD是∠ACB的平分线,∠EDC=25,∠DCE=25,∠B=70.
(1)试证明:DE∥BC;
(2)求∠BDC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,矩形
 的顶点
的顶点 的坐标分别为
的坐标分别为 ,
, ,
,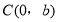 ,且
,且 满足
满足 ;
;(1)矩形的顶点
 的坐标是( , ).
的坐标是( , ).(2)若
 是
是 中点,沿
中点,沿 折叠矩形
折叠矩形 使
使 点落在
点落在 处,折痕为
处,折痕为 ,连
,连 并延长交
并延长交 于
于 ,求直线
,求直线 的解析式.
的解析式.(3)将(2)中直线
 向左平移
向左平移 个单位交
个单位交 轴于
轴于 ,
, 为第二象限内的一个动点,且
为第二象限内的一个动点,且 ,求
,求 的最大值.
的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示,则下列结论:①4a﹣b=0;②c<0;③﹣3a+c>0;④4a﹣2b>at2+bt(t为实数);⑤点(﹣
 ,y1),(﹣
,y1),(﹣  ,y2),(﹣
,y2),(﹣  ,y3)是该抛物线上的点,则y1<y2<y3 , 正确的个数有( )
,y3)是该抛物线上的点,则y1<y2<y3 , 正确的个数有( ) 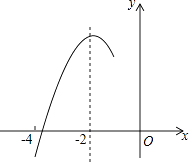
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A.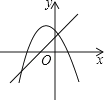
B.
C.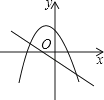
D.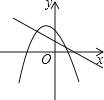
相关试题

