【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示,则下列结论:①4a﹣b=0;②c<0;③﹣3a+c>0;④4a﹣2b>at2+bt(t为实数);⑤点(﹣ ![]() ,y1),(﹣
,y1),(﹣ ![]() ,y2),(﹣
,y2),(﹣ ![]() ,y3)是该抛物线上的点,则y1<y2<y3 , 正确的个数有( )
,y3)是该抛物线上的点,则y1<y2<y3 , 正确的个数有( ) 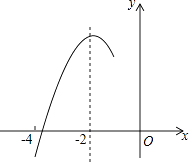
A.4个
B.3个
C.2个
D.1个
参考答案:
【答案】B
【解析】解:∵抛物线的对称轴为直线x=﹣ ![]() =﹣2, ∴4a﹣b=0,所以①正确;
=﹣2, ∴4a﹣b=0,所以①正确;
∵与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,
∴由抛物线的对称性知,另一个交点在(﹣1,0)和(0,0)之间,
∴抛物线与y轴的交点在y轴的负半轴,即c<0,故②正确;
∵由②知,x=﹣1时y>0,且b=4a,
即a﹣b+c=a﹣4a+c=﹣3a+c>0,
所以③正确;
由函数图象知当x=﹣2时,函数取得最大值,
∴4a﹣2b+c≥at2+bt+c,
即4a﹣2b≥at2+bt(t为实数),故④错误;
∵抛物线的开口向下,且对称轴为直线x=﹣2,
∴抛物线上离对称轴水平距离越小,函数值越大,
∴y1<y3<y2 , 故⑤错误;
故选:B.
【考点精析】根据题目的已知条件,利用二次函数的性质和二次函数图象以及系数a、b、c的关系的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).
-
科目: 来源: 题型:
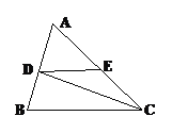
查看答案和解析>>【题目】如图,CD是∠ACB的平分线,∠EDC=25,∠DCE=25,∠B=70.
(1)试证明:DE∥BC;
(2)求∠BDC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,AB⊥BC,AB=BC,AB>CD,AE⊥BD于E交BC于F.

(1)若AB=2CD;
①求证:BC=2BF;
②连CE,若DE=6,CE=
 ,求EF的长;
,求EF的长;(2)若AB=6,则CE的最小值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,矩形
 的顶点
的顶点 的坐标分别为
的坐标分别为 ,
, ,
,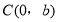 ,且
,且 满足
满足 ;
;(1)矩形的顶点
 的坐标是( , ).
的坐标是( , ).(2)若
 是
是 中点,沿
中点,沿 折叠矩形
折叠矩形 使
使 点落在
点落在 处,折痕为
处,折痕为 ,连
,连 并延长交
并延长交 于
于 ,求直线
,求直线 的解析式.
的解析式.(3)将(2)中直线
 向左平移
向左平移 个单位交
个单位交 轴于
轴于 ,
, 为第二象限内的一个动点,且
为第二象限内的一个动点,且 ,求
,求 的最大值.
的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A.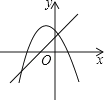
B.
C.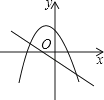
D.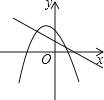
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知l1∥l2,MN分别和直线l1、l2交于点A、B,ME分别和直线l1、l2交于点C、D,点P在MN上(P点与A、B、M三点不重合).
(1)如果点P在A、B两点之间运动时,∠α、∠β、∠γ之间有何数量关系请说明理由;
(2)如果点P在A、B两点外侧运动时,∠α、∠β、∠γ有何数量关系(只须写出结论).

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)(x3)2.(﹣x4)3
(2)(
 x5y4﹣
x5y4﹣ x4y3)
x4y3) x3y3
x3y3(3)(2a+1)2﹣(2a+1)(2a﹣1)
(4)102+
 ×(π﹣3.14)0﹣|﹣302|
×(π﹣3.14)0﹣|﹣302|
相关试题

