【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),对称轴l如图所示,则下列结论:①abc>0;②a﹣b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( ) 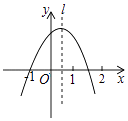
A.①③
B.②③
C.②④
D.②③④
参考答案:
【答案】D
【解析】解:①∵二次函数图象的开口向下, ∴a<0,
∵二次函数图象的对称轴在y轴右侧,
∴﹣ ![]() >0,
>0,
∴b>0,
∵二次函数的图象与y轴的交点在y轴的正半轴上,
∴c>0,
∴abc<0,故①错误;
②∵抛物线y=ax2+bx+c经过点(﹣1,0),
∴a﹣b+c=0,故②正确;
③∵a﹣b+c=0,∴b=a+c.
由图可知,x=2时,y<0,即4a+2b+c<0,
∴4a+2(a+c)+c<0,
∴6a+3c<0,∴2a+c<0,故③正确;
④∵a﹣b+c=0,∴c=b﹣a.
由图可知,x=2时,y<0,即4a+2b+c<0,
∴4a+2b+b﹣a<0,
∴3a+3b<0,∴a+b<0,故④正确.
故选D.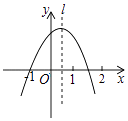
【考点精析】本题主要考查了二次函数图象以及系数a、b、c的关系的相关知识点,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线y=ax2+bx+c的顶点为B(﹣1,3),与x轴的交点A在点(﹣3,0)和(﹣2,0)之间,以下结论: ①b2﹣4ac=0;②a+b+c>0;③2a﹣b=0;④c﹣a=3
其中正确的有( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如下,则一次函数y=ax﹣2b与反比例函数y=
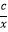 在同一平面直角坐标系中的图象大致是( )
在同一平面直角坐标系中的图象大致是( )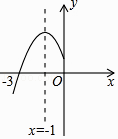
A.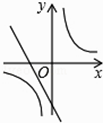
B.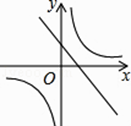
C.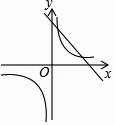
D.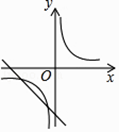
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为正方形,DE∥AC且CE=CA,直线EC交DA延长线于F.

(1)若CD=6,求DE的长;
(2)求证:AE=AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2013次,点P依次落在点
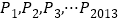 的位置,记
的位置,记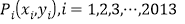 ,则P2013的横坐标x2013=______;如果
,则P2013的横坐标x2013=______;如果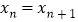 ,则
,则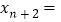 ______(请用含有n的式子表示).
______(请用含有n的式子表示).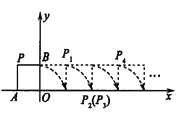
-
科目: 来源: 题型:
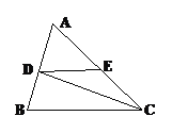
查看答案和解析>>【题目】如图,CD是∠ACB的平分线,∠EDC=25,∠DCE=25,∠B=70.
(1)试证明:DE∥BC;
(2)求∠BDC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,AB⊥BC,AB=BC,AB>CD,AE⊥BD于E交BC于F.

(1)若AB=2CD;
①求证:BC=2BF;
②连CE,若DE=6,CE=
 ,求EF的长;
,求EF的长;(2)若AB=6,则CE的最小值为______.
相关试题

