【题目】在数轴上,O表示原点,A、B两点分别表示﹣8和2.
(1)求出线段AB的长度;
(2)动点P从A出发沿数轴向右运动,速度为每秒5个单位长度;同时点Q从B出发,沿数轴向右运动,速度为每秒3个单位长度,当P、Q重合时,两点同时停止运动.设两点运动时间为t秒,用含有t的式子表示线段PQ的长;
(3)在(2)的条件下,t为何值时,点P、点Q到原点O的距离相等.

参考答案:
【答案】(1)AB=10;(2) PQ=10﹣2t且0≤t≤5;(3)为0.75、5时,点P、点Q到原点O的距离相等.
【解析】
(1)用点A到原点O的距离加上点B到原点O的距离,即可求出线段AB的长度.
(2)用线段AB的长度减去动点P向右运动的长度,再加上动点Q向右运动的长度,用含有t的代数式表示线段PQ的长即可.
(3)根据题意,分两种情况:①点P、点Q重合时;②点P、点Q在原点O的两侧时;求出t为何值时,点P、点Q到原点O的距离相等即可.
(1)AB=OA+OB=8+2=10,
(2)PQ=10﹣5t+3t=10﹣2t,
由10﹣2t≥0,
解得0≤t≤5.
(3)①点P、点Q重合时,
由10﹣2t=0,
解得t=5.
②点P、点Q在原点O的两侧时,
OP=8﹣5t,
OQ=2+3t,
由8﹣5t=2+3t,
解得t=0.75,
所以t为0.75、5时,点P、点Q到原点O的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
(1)如图②,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图③,点B、C分别在∠MAN的边AM、AN上,点E、F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE与△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF.
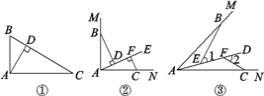
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E . 若∠A=60°,BC=6,则图中阴影部分的面积为

A. π
π
B. π
π
C. π
π
D.3π -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为2,对角线AC与BC相交于O , E为AB的中点,F为DE的中点,G为CF的中点, OH⊥DE于H , 过A作AI⊥DE于I , 交BD于J , 交BC于K , 连接BI .
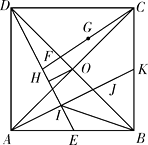
下列结论:①G到AC的距离等于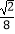 ;②OH=
;②OH=  ;③BK=
;③BK=  AK;④∠BIJ=45°.其中正确的结论是
AK;④∠BIJ=45°.其中正确的结论是
A.①②③
B.①②④
C.①③④
D.①②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,BC=6,分别以点A和点C为圆心,以相同的长(大于
 AC)为半径作弧,两弧相交于点M和点N , 作直线MN交AB于点D , 交AC于点E , 连接CD . 则DE的长为 .
AC)为半径作弧,两弧相交于点M和点N , 作直线MN交AB于点D , 交AC于点E , 连接CD . 则DE的长为 . 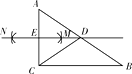
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的两个顶点A , D分别在x轴和y轴上,CE⊥y轴于点E , OA=2,∠ODA=30°.若反比例函数y=
 的图象过CE的中点F , 则k的值为 .
的图象过CE的中点F , 则k的值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)

(2)(2x)2x4÷x
(3)

(4)

(5)(x﹣2)(2+x)﹣(2﹣x)(x﹣2)
(6)(6x4y2+8x3y4)÷2xy2﹣(﹣2xy)2
相关试题

