【题目】某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
参考答案:
【答案】解:如图作CM∥AB交AD于M,MN⊥AB于N.

由题意 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,CM=
,CM= ![]() ,
,
在RT△AMN中,∵∠ANM=90°,MN=BC=4,∠AMN=72°,
∴tan72°= ![]() ,
,
∴AN≈12.3,
∵MN∥BC,AB∥CM,
∴四边形MNBC是平行四边形,
∴BN=CM= ![]() ,
,
∴AB=AN+BN=13.8米.
【解析】作CM∥AB交AD于M,MN⊥AB于N.首先可证明△RPQ∽△DMC,依据相似三角形的性质可得到CM的长,然后在RT△AMN中依据锐角三角形函数的定义求得AN的长,最后依据AB=AN+BN求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,解答下面的问题:
我们知道方程
 有无数个解,但在实际生活中我们往往只需求出其
有无数个解,但在实际生活中我们往往只需求出其正整数解.
例:由
 ,得:
,得: ,(x、y为正整数)
,(x、y为正整数)∴
 ,则有
,则有 .又
.又 为正整数,则
为正整数,则 为正整数.由2与3互质,可知:x为3的倍数,从而x=3,代入
为正整数.由2与3互质,可知:x为3的倍数,从而x=3,代入 ∴2x+3y=12的正整数解为
∴2x+3y=12的正整数解为
问题:
(1)请你写出方程
 的一组正整数解: .
的一组正整数解: .(2)若
 为自然数,则满足条件的x值为 .
为自然数,则满足条件的x值为 .(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在进行二次根式化简时,我们有时会碰上如
 ,
, ,
, 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: =
=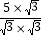 =
= ,
, =
= =
= ,
, =
= =
= =
= -1,
-1, 还可以用以下方法化简:
还可以用以下方法化简: =
= =
= =
= =
= -1.以上这种化简的方法叫做分母有理化.(1)请化简
-1.以上这种化简的方法叫做分母有理化.(1)请化简 =________;(2)若a是
=________;(2)若a是 的小数部分则
的小数部分则 =________;(3)矩形的面积为3
=________;(3)矩形的面积为3 +1,一边长为
+1,一边长为 -2,则它的周长为________;(4)化简
-2,则它的周长为________;(4)化简 +
+ +
+ +…+
+…+ .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正五边形ABCDE中,直线
 过点B,且
过点B,且 ⊥ED,下列说法:①
⊥ED,下列说法:① 是线段AC的垂直平分线;②∠BAC=36°;③正五边形ABCDE有五条对称轴.正确的有( ).
是线段AC的垂直平分线;②∠BAC=36°;③正五边形ABCDE有五条对称轴.正确的有( ).
A. ①②B. ①③C. ②③D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点
 ,第二次点
,第二次点 跳动至点
跳动至点 第三次点
第三次点 跳动至点
跳动至点 ,第四次点
,第四次点 跳动至点
跳动至点 ……,依此规律跳动下去,则点
……,依此规律跳动下去,则点 与点
与点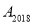 之间的距离是( )
之间的距离是( )
A. 2017B. 2018C. 2019D. 2020
-
科目: 来源: 题型:
查看答案和解析>>【题目】假期,某校为了勤工俭学,要完成整个A小区的绿化工作,开始由七年级单独工作了4天,完成整个绿化工作的三分之一,这时九年级也参加工作,两个年级又共同工作了2天,才全部完成整个绿化工作,则由九年级单独完成整个绿化工作需要____天.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张长方形的纸条ABCD沿EF折叠,AD交
 于点G,若折叠后
于点G,若折叠后
(1)求∠CEF的度数;
(2)求证:△EFG是等腰三角形.

相关试题

