搜索
【题目】如图，正五边形ABCDE中，直线
过点B，且⊥ED，下列说法：①是线段AC的垂直平分线；②∠BAC=36°；③正五边形ABCDE有五条对称轴.正确的有（ ）.
A. ①②B. ①③C. ②③D. ①②③
参考答案：
【答案】D
【解析】
根据等腰三角形的性质可得
是线段AC的垂直平分线；根据多边形内角和定理可得∠ABC=108°，进而根据等腰三角形的性质求出∠BAC=36°；过正五边形的每个顶点且垂直于对边的直线都是正五边形的对称轴，综上即可得答案.
∵AB=BC，直线过点B，且⊥ED，
∴是线段AC的垂直平分线；故①正确，
∵正五边形的内角和=（5-2）×180°=540°，
∴∠ABC=108°，
∵AB=BC，
∴∠BAC=36°，故②正确，
∵过正五边形的每个顶点且垂直于对边的直线都是正五边形的对称轴，
∴正五边形ABCDE有五条对称轴.故③正确，
故说法正确的有①②③，
故选D
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料，回答有关问题：在实数这章中，遇到过
，
，
，
，
这样的式子，我们把这样的式子叫做二次根式，根号下的数叫做被开方数．如果一个二次根式的被开方数中有的因数能开得尽方，可以利用
＝
(a≥0，b≥0)；
(a≥0，b>0)将这些因数开出来，从而将二次根式化简．当一个二次根式的被开方数中不含开得尽方的因数或者被开方数中不含有分母时，这样的二次根式叫做最简二次根式，例如，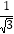
化成最简二次根式是
，
化成最简二次根式是3，几个二次根式化成最简二次根式以后，如果被开方数相同，这几个二次根式叫做同类二次根式，如上面的例子中的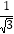和就是同类二次根式．(1)请判断下列各式中，哪些是同类二次根式？
，
，
，
，
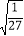，.(2)二次根式中的同类二次根式可以像整式中的同类项一样合并，请计算：
＋－－＋－. -
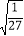科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料，解答下面的问题：
我们知道方程
有无数个解，但在实际生活中我们往往只需求出其正整数解．
例：由
，得：
，（x、y为正整数）∴
，则有
．又
为正整数，则
为正整数．由2与3互质，可知：x为3的倍数，从而x=3，代入
∴2x+3y=12的正整数解为
问题：
（1）请你写出方程
的一组正整数解： .（2）若
为自然数，则满足条件的x值为 .（3）七年级某班为了奖励学习进步的学生，购买了单价为3元的笔记本与单价为5元的钢笔两种奖品，共花费35元，问有几种购买方案？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在进行二次根式化简时，我们有时会碰上如
，
，
一样的式子，其实我们还可以将其进一步化简：＝
＝
，＝
＝
，＝
＝
＝
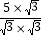－1，还可以用以下方法化简：＝
＝
＝
＝－1.以上这种化简的方法叫做分母有理化．(1)请化简
＝________；(2)若a是
的小数部分则
＝________；(3)矩形的面积为3
＋1，一边长为－2，则它的周长为________；(4)化简
＋
＋
＋…＋
. -
科目： 来源： 题型：
查看答案和解析>>【题目】某中学广场上有旗杆如图1所示，在学习解直角三角形以后，数学兴趣小组测量了旗杆的高度．如图2，某一时刻，旗杆AB的影子一部分落在平台上，另一部分落在斜坡上，测得落在平台上的影长BC为4米，落在斜坡上的影长CD为3米，AB⊥BC，同一时刻，光线与水平面的夹角为72°，1米的竖立标杆PQ在斜坡上的影长QR为2米，求旗杆的高度（结果精确到0.1米）．（参考数据：sin72°≈0.95，cos72°≈0.31，tan72°≈3.08）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系上有点A(1，0)，点A第一次跳动至点
，第二次点
跳动至点
第三次点
跳动至点
，第四次点
跳动至点
……，依此规律跳动下去，则点
与点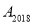
之间的距离是（ ）
A. 2017B. 2018C. 2019D. 2020
-
科目： 来源： 题型：
查看答案和解析>>【题目】假期，某校为了勤工俭学,要完成整个A小区的绿化工作，开始由七年级单独工作了4天，完成整个绿化工作的三分之一，这时九年级也参加工作，两个年级又共同工作了2天，才全部完成整个绿化工作，则由九年级单独完成整个绿化工作需要____天.
相关试题
