【题目】如图,将一张长方形的纸条ABCD沿EF折叠,AD交![]() 于点G,若折叠后
于点G,若折叠后![]()
(1)求∠CEF的度数;
(2)求证:△EFG是等腰三角形.

参考答案:
【答案】(1)∠CEF=66°;(2)证明见解析;
【解析】
(1)根据平行线性质可得∠BEC′=∠AGC′,由折叠的性质可得∠FEC′=∠CEF,根据平角的性质求出∠CEF的度数即可;(2)根据平行线性质可得∠EFG=∠FEC,根据折叠性质可得∠CEF=∠GEF,由等量代换可证明∠GEF=∠GFE,进而可得答案.
(1)∵AG//BE,∠AGC′=48°,
∴∠BEC′=∠AGC′=48°,
∵由折叠的性质得:∠FEC′=∠CEF,
∴∠CEF=![]() (180°-∠BEC′)=66°.
(180°-∠BEC′)=66°.
(2)∵DG//CE,
∴∠EFG=∠CEF,
∵∠CEF=∠GEF,
∴∠EFG=∠GEF,
∴EG=FG,
∴△EFG是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点
 ,第二次点
,第二次点 跳动至点
跳动至点 第三次点
第三次点 跳动至点
跳动至点 ,第四次点
,第四次点 跳动至点
跳动至点 ……,依此规律跳动下去,则点
……,依此规律跳动下去,则点 与点
与点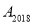 之间的距离是( )
之间的距离是( )
A. 2017B. 2018C. 2019D. 2020
-
科目: 来源: 题型:
查看答案和解析>>【题目】假期,某校为了勤工俭学,要完成整个A小区的绿化工作,开始由七年级单独工作了4天,完成整个绿化工作的三分之一,这时九年级也参加工作,两个年级又共同工作了2天,才全部完成整个绿化工作,则由九年级单独完成整个绿化工作需要____天.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆轿车和一辆货车同时从甲地出发,已知轿车的速度比货车的速度每小时快20千米,当轿车行驶到距甲地360千米的丙地时,货年恰好行驶到距离甲地300千米的乙地,问轿车与货车的速度分别是多少?
-
科目: 来源: 题型:
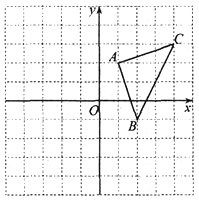
查看答案和解析>>【题目】如图,平面直角坐标系中,△ABC的顶点坐标为:A(1,2),B(2, 一1), C (4, 3).
(1)将△ABC向左平移2个单位长度,再向上平移1个单位长度,得△A'B'C'.画出△A'B'C',并写出△A'B'C'的顶点坐标;
(2)求△ABC的面积.
-
科目: 来源: 题型:
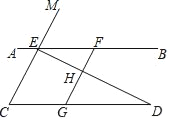
查看答案和解析>>【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.
相关试题

