【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择,李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站 | A | B | C | D | E |
x(千米) | 8 | 9 | 10 | 11.5 | 13 |
y1(分钟) | 18 | 20 | 22 | 25 | 28 |
(1)求y1关于x的函数表达式;
(2)李华骑单车的时间(单位:分钟)也受x的影响,其关系可以用y2= ![]() x2﹣11x+78来描述,请问:李华应选择在那一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
x2﹣11x+78来描述,请问:李华应选择在那一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
参考答案:
【答案】
(1)解:设y1=kx+b,将(8,18),(9,20),代入得:
![]() ,
,
解得: ![]() ,
,
故y1关于x的函数表达式为:y1=2x+2
(2)解:设李华从文化宫回到家所需的时间为y,则
y=y1+y2=2x+2+ ![]() x2﹣11x+78=
x2﹣11x+78= ![]() x2﹣9x+80,
x2﹣9x+80,
∴当x=9时,y有最小值,ymin= 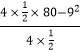 =39.5,
=39.5,
答:李华应选择在B站出地铁,才能使他从文化宫回到家所需的时间最短,最短时间为39.5分钟
【解析】(1)根据表格中的数据,运用待定系数法,即可求得y1关于x的函数表达式;(2)设李华从文化宫回到家所需的时间为y,则y=y1+y2= ![]() x2﹣9x+80,根据二次函数的性质,即可得出最短时间.
x2﹣9x+80,根据二次函数的性质,即可得出最短时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先化简,再求值: 2(m2 mn 1) 3(
 m2 2mn 4) ,其中 m
m2 2mn 4) ,其中 m  ,n 3 .
,n 3 .(2)已知 2a b 5 0 ,求整式 6a b 与 2a 3b 27 的和的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于
 MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为 .
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为 . 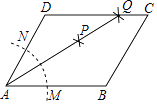
-
科目: 来源: 题型:
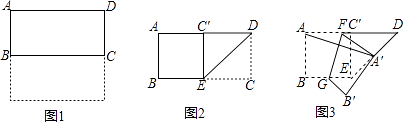
查看答案和解析>>【题目】如图1,把一张正方形纸片对折得到长方形ABCD,再沿∠ADC的平分线DE折叠,如图2,点C落在点C′处,最后按图3所示方式折叠,使点A落在DE的中点A′处,折痕是FG,若原正方形纸片的边长为6cm,则FG=cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=
 ∠BAC=60°,于是
∠BAC=60°,于是  =
= 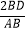 =
= 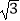 ; 迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠ADE=120°,D,E,C三点在同一条直线上,连接BD.
; 迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠ADE=120°,D,E,C三点在同一条直线上,连接BD.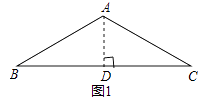
(1)①求证:△ADB≌△AEC;②请直接写出线段AD,BD,CD之间的等量关系式;
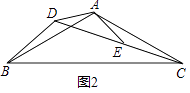
(2)拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.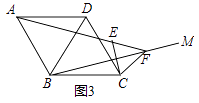
①证明△CEF是等边三角形;
②若AE=5,CE=2,求BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系xOy中,抛物线C:y=ax2+bx+c与x轴相交于A,B两点,顶点为D(0,4),AB=4
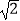 ,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C′.
,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C′.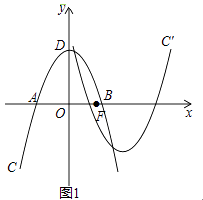
(1)求抛物线C的函数表达式;
(2)若抛物线C′与抛物线C在y轴的右侧有两个不同的公共点,求m的取值范围.
(3)如图2,P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C′上的对应点P′,设M是C上的动点,N是C′上的动点,试探究四边形PMP′N能否成为正方形?若能,求出m的值;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OD 是∠AOB 的平分线,∠AOC=2∠BOC.
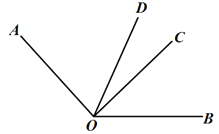
(1)若 AO⊥CO,求∠BOD 的度数;
(2)若∠COD=21°,求∠AOB 的度数.
相关试题

