【题目】如图,OD 是∠AOB 的平分线,∠AOC=2∠BOC.
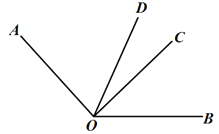
(1)若 AO⊥CO,求∠BOD 的度数;
(2)若∠COD=21°,求∠AOB 的度数.
参考答案:
【答案】(1)67.5![]() , (2)126
, (2)126![]() .
.
【解析】
(1)由垂直可得∠AOC=90°,由∠AOC=2∠BOC得∠BOC的度数,即可得∠AOB的度数,然后根据角平分线的定义可知∠AOD=∠BOD=![]() ,计算即可求出;
,计算即可求出;
(2)由∠AOC=2∠BOC得∠AOB=3∠BOC ,然后根据角平分线的定义可知∠AOD=∠BOD=![]() ,再由∠COD=∠BOD-∠BOC =21°可先求得∠BOC,即可得∠AOB 的度数.
,再由∠COD=∠BOD-∠BOC =21°可先求得∠BOC,即可得∠AOB 的度数.
(1)∵AO![]()
∵∠AOC=90°
∵∠AOC=2∠BOC
∴∠BOC=45°
∴∠AOB=∠AOC+∠BOC=135![]()
∵OD平分∠AOB
∴∠BOD=![]() =67.5
=67.5![]() ;
;
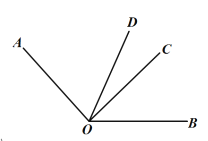
(2)∵∠AOC=2∠BOC
∴∠AOB=∠AOC+∠BOC =3∠BOC
∵OD平分∠AOB
∴∠BOD=![]() ∠AOB=
∠AOB=![]() ∠BOC
∠BOC
∴∠COD=∠BOD-∠BOC=![]() ∠BOC
∠BOC
∵∠COD=21![]()
∴∠BOC=42°
∴∠AOB =3∠BOC = 126![]() .
.
故答案为:(1)67.5![]() , (2)126
, (2)126![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择,李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站
A
B
C
D
E
x(千米)
8
9
10
11.5
13
y1(分钟)
18
20
22
25
28
(1)求y1关于x的函数表达式;
(2)李华骑单车的时间(单位:分钟)也受x的影响,其关系可以用y2= x2﹣11x+78来描述,请问:李华应选择在那一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
x2﹣11x+78来描述,请问:李华应选择在那一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=
 ∠BAC=60°,于是
∠BAC=60°,于是  =
= 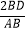 =
= 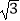 ; 迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠ADE=120°,D,E,C三点在同一条直线上,连接BD.
; 迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠ADE=120°,D,E,C三点在同一条直线上,连接BD.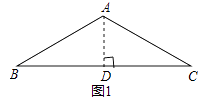
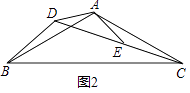
(1)①求证:△ADB≌△AEC;②请直接写出线段AD,BD,CD之间的等量关系式;
(2)拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.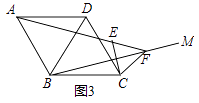
①证明△CEF是等边三角形;
②若AE=5,CE=2,求BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系xOy中,抛物线C:y=ax2+bx+c与x轴相交于A,B两点,顶点为D(0,4),AB=4
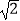 ,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C′.
,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C′.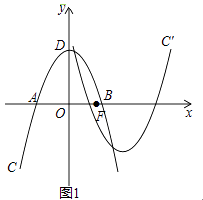
(1)求抛物线C的函数表达式;
(2)若抛物线C′与抛物线C在y轴的右侧有两个不同的公共点,求m的取值范围.
(3)如图2,P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C′上的对应点P′,设M是C上的动点,N是C′上的动点,试探究四边形PMP′N能否成为正方形?若能,求出m的值;若不能,请说明理由.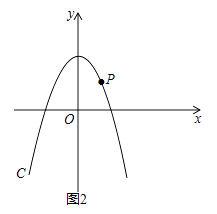
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从 A,B 两地同时出发,沿同一条路线相向匀速行驶.出发后经 2 小时两车相遇, 已知在相遇时乙车比甲车多行驶了 30 千米.相遇后若乙车继续往前行驶,还需 1.6 小时才能 到达 A 地.
(1)求甲,乙两车行驶的速度分别是多少?
(2)如果相遇后甲车继续前往 B 地(到达后停止行驶),乙车在相遇点休息了 10 分钟后,按 原速度立即返回 B 地,问乙车重新出发后多长时间,两车相距 5 千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段 AB a .延长线段 BA 到点 C,使 AC=2AB,延长线段 AB 到点 E,使 BE=
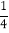 BC.
BC.
(1)用刻度尺按要求补全图形;
(2)图中有几条线段?求出所有线段的长度和(用含 a 的代数式表示);
(3)点 D 是 CE 的中点,若 AD=0.5cm,求 a 的值.
相关试题

