【题目】(1)先化简,再求值: 2(m2 mn 1) 3(![]() m2 2mn 4) ,其中 m
m2 2mn 4) ,其中 m ![]() ,n 3 .
,n 3 .
(2)已知 2a b 5 0 ,求整式 6a b 与 2a 3b 27 的和的值.
参考答案:
【答案】(1)-16,(2)17
【解析】
(1)原式去括号合并得到最简结果,把m与n的值代入计算即可求出值;
(2)先根据整式的加减计算整式 6a b 与 2a 3b 27 的和,再由已知得2a b=-5,把2a b=-5代入计算即可求出值.
(1)原式=2![]() -2mn+2-2
-2mn+2-2![]() +6mn-12=4mn-10,
+6mn-12=4mn-10,
当m=![]() ,n=-3时,原式4mn-10=4
,n=-3时,原式4mn-10=4![]() ;
;
(2)(6a+b)+(-2a-3b+27)=6a+b-2a-3b+27=4a-2b+27,
∵ 2a-b+5=0
∴2a-b=-5
∴ (6a+b)+(-2a-3b+27=4a-2b+27
=2(2a-b)+27
= 2![]() .
.
故答案为:(1)-16,(2)17 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(13分)(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得线段BE、EF、FD之间的数量关系为 .
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=
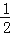 ∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?(3)如图3,点A在点O的北偏西30°处,点B在点O的南偏东70°处,且AO=BO,点A沿正东方向移动249米到达E处,点B沿北偏东50°方向移动334米到达点F处,从点O观测到E、F之间的夹角为70°,根据(2)的结论求E、F之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知 A,B,C 三点都在直线l 上,AC 与 BC 的长度之比为 2:3,D 是 AB 的中点.若 AC4cm,则 CD 的长为 ________________ cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从大拇指开始,按照大拇指→食指→中指→无名指→小指→无名指→中指→食指→大拇指→ 食指的顺序,依次数整数 1,2,3,4,5,6,7,,当数到 2019 时,对应的手指为________________; 当第 n 次数到食指时,数到的数是_________________________ (用含 n 的代数式表示).
-
科目: 来源: 题型:
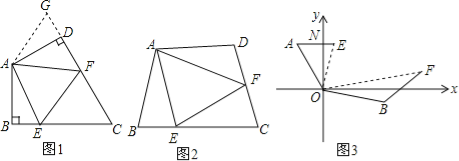
查看答案和解析>>【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于
 MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为 .
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,把一张正方形纸片对折得到长方形ABCD,再沿∠ADC的平分线DE折叠,如图2,点C落在点C′处,最后按图3所示方式折叠,使点A落在DE的中点A′处,折痕是FG,若原正方形纸片的边长为6cm,则FG=cm.
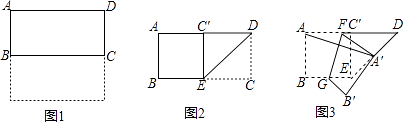
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择,李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站
A
B
C
D
E
x(千米)
8
9
10
11.5
13
y1(分钟)
18
20
22
25
28
(1)求y1关于x的函数表达式;
(2)李华骑单车的时间(单位:分钟)也受x的影响,其关系可以用y2= x2﹣11x+78来描述,请问:李华应选择在那一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
x2﹣11x+78来描述,请问:李华应选择在那一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
相关试题

