【题目】细心观察下图,认真分析各式,然后解答问题.
(![]() )2+1=2,S1=
)2+1=2,S1=![]() ;
;
(![]() )2+1=3,S2=
)2+1=3,S2=![]() ;
;
(![]() )2+1=4,S3=
)2+1=4,S3=![]() .
.
(1)请用含n(n是正整数)的等式表示上述式子的变化规律;
(2)推算出OA10的长;
(3)求出S12+S22+S32+…+S102的值.

参考答案:
【答案】(1)(![]() )2+1=n+1,Sn=
)2+1=n+1,Sn=![]() (n是正整数);(2)
(n是正整数);(2) ![]() ;(3)
;(3) ![]() .
.
【解析】(1)利用已知可得OAn2,注意观察数据的变化,
即:![]() +1=n+1,Sn=
+1=n+1,Sn=![]() (n是正整数).
(n是正整数).
(2)结合(1)中规律即可求出OA102的值,即可求出OA10=![]() .
.
(3)将前10个三角形面积相加,利用数据的特殊性即可求出.
(1) ![]() +1=n+1,Sn=
+1=n+1,Sn=![]() (n是正整数).
(n是正整数).
(2)∵OA1=![]() ,OA2=
,OA2=![]() ,OA3=
,OA3=![]() ,…∴OA10=
,…∴OA10=![]() .
.
(3)S12+S22+S32+…+S102=![]() +
+![]() +
+![]() +…+
+…+![]()
=![]() (1+2+3+…+10)
(1+2+3+…+10)
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小林在某商店购买商品A、B若干次(每次A、B两种商品都购买),其中第一、二两次购买时,均按标价购买;第三次购买时,商品A、B同时打折.三次购买商品A、B的数量和费用如表所示.
购买商品A的数量/个
购买商品B的数量/个
购买总费用/元
第一次购物
6
5
980
第二次购物
3
7
940
第三次购物
9
8
912
(1)求商品A、B的标价;
(2)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
(3)在(2)的条件下,若小林第四次购物共花去了960元,则小林有哪几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在求值问题中,我们经常遇到利用整体思想来解决问题.
例如1:已知:x+2y﹣3z=2,2x+y+6z=1,求:x+y+z的值
解:令x+2y﹣3z=2﹣﹣﹣﹣﹣①2x+y+6z=1﹣﹣﹣﹣﹣﹣②
①+②得3x+3y+3z=3所以x+y+z=1
已知
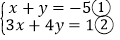 求x+2y的值
求x+2y的值解:①×2得:2x+2y=﹣10③
②﹣③得:x+2y=11
利用材料中提供的方法,解决下列问题
(1)已知:关于x,y的二元一次方程组
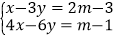 的解满足x﹣y=6,求m的值
的解满足x﹣y=6,求m的值(2)某步行街摆放有若干盆甲、乙、丙三种造型的盆景.甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成,乙种盆景由10朵红花和12朵黄花搭配而成,丙咱盆景由10朵红花、18朵黄花和25朵紫花搭配而成.这些盆景一共用了2900朵红花,3750朵紫花,求黄花一共用了多少朵?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数a,b,c满足(a-
 )2+
)2+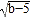 +|c-2
+|c-2 |=0.
|=0.(1)求a,b,c的值;
(2)试问以a,b,c为边能否构成三角形?若能构成三角形,求出三角形的周长和面积;若不能构成三角形,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)4x+3(2x﹣3)=12﹣(x﹣4)
(2)

(3)

-
科目: 来源: 题型:
查看答案和解析>>【题目】解答下列问题:
(1)一项工程,甲队单独做需10天完成,乙队单独做需15天完成,甲先做5天后,甲、乙合作完成余下的工作,问两队合做几天可以完成这项工作?
(2)从A地到B地,甲需走10小时,从B地到A地,乙需走15小时,甲、乙两人从A,B两地相向而行,甲出发5小时后乙出发,问乙出发几小时后两人相遇?
(3)一笔钱款,可以买甲种商品10件或买乙种商品15件,用这笔钱款买了甲、乙两种商品,已知甲种商品比乙种商品多买了5件,问乙种商品买了几件?
(4)通过解答上面三个问题,你发现了什么?
(5)根据上面所列的方程,编写一道实际问题的应用题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图
【1】求这10个样本数据的平均数、众数和中位数;
【2】根据样本数据,估计小刚所在班50名同学家庭中月均用水量不超过7 t的约有多少户.
相关试题

