【题目】我们用![]() 表示不大于
表示不大于![]() 的最大整数,例如:
的最大整数,例如:![]() ,
,![]() ,
,![]() ;用
;用![]() 表示大于
表示大于![]() 的最小整数,例如:
的最小整数,例如:![]() ,
,![]() ,
,![]() .解决下列问题:
.解决下列问题:
(1)![]() = ,,
= ,,![]() = ;
= ;
(2)若![]() =2,则
=2,则![]() 的取值范围是 ;若
的取值范围是 ;若![]() =-1,则
=-1,则![]() 的取值范围是 ;
的取值范围是 ;
(3)已知![]() ,
,![]() 满足方程组
满足方程组![]() ,求
,求![]() ,
,![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)-5,4;(2)![]() ,
,![]() ;(3)
;(3)![]() ,
,![]() .
.
【解析】
试题(1)根据题目条件:用[a]表示不大于a的最大整数,用<a>表示大于a的最小整数,可分别求解;(2)根据[a]表示不大于a的最大整数,可得[x]=2中的2≤x<3,根据<a>表示大于a的最小整数,可得<y>=-1中,-2≤y<-1;(3)先解方程组,求出[x]和<y>的值,然后求出x和y的取值范围.
试题解析:
解:(1)由题意得,[-4.5]=-5,<3.5>=4;
(2)因为[a]表示不大于a的最大整数且[x]=2,所以x的取值范围是2≤x<3;
因为<a>表示大于a的最小整数,且<y>=-1, 所以y的取值范围是-2≤y<-1;
(3)解方程组![]() 得:
得:
[x]="-1," <y>=3 所以x,y的取值范围分别为-1≤x<0,2≤y<3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在升旗结束后,小铭想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好至C处且与地面成60°角,小铭从绳子末端C处拿起绳子后退至E点,求旗杆AB的高度和小铭后退的距离.(单位:米,参考数据:
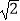 ≈1.41,
≈1.41,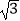 ≈1.73,结果保留一位小数)
≈1.73,结果保留一位小数)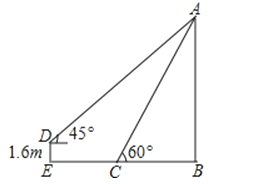
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注,某学校计划在教室内安装空气净化装置,需购进A、B两种设备,已知:购买1台A种设备和2台B种设备需要3.5万元;购买2台A种设备和1台B种设备需要2.5万元.
(1)求每台A种、B种设备各多少万元?
(2)根据学校实际,需购进A种和B种设备共30台,总费用不超过30万元,请你通过计算,求至少购买A种设备多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°.如果将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处.那么旋转的角度等于( )

A.55°
B.60°
C.65°
D.80° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图①,△ABC是等边三角形,点D、E分别在边AB、BC上,且BD=BE,连接DE.
(1)求证:DE∥AC;
(2)将图①中的△BDE绕点B顺时针旋转,使得点A、D、E在同一条直线上,如图②,求∠AEC的度数;
(3)在(2)的条件下,如图③,连接CD,过点D作DM⊥BE于点M,在线段BM上取点N,使得∠DNE+∠DCE=180°.求证:EN﹣EC=2MN.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,一次函数
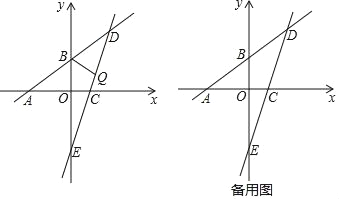
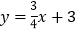 的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.(1)直线CD的函数表达式为 ;(直接写出结果)
(2)点Q为线段DE上的一个动点,连接BQ.
①若直线BQ将△BDE的面积分为1:2两部分,试求点Q的坐标;
②将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的坐标轴上,请直接写出点Q的坐标: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学进行了6轮投篮比赛,两人的得分情况统计如下:
第1轮
第2轮
第3轮
第4轮
第5轮
第6轮
甲
10
14
12
18
16
20
乙
12
11
9
14
22
16
下列说法不正确的是( )
A.甲得分的极差小于乙得分的极差
B.甲得分的中位数大于乙得分的中位数
C.甲得分的平均数大于乙得分的平均数
D.乙的成绩比甲的成绩稳定
相关试题

