【题目】如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.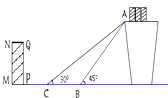
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物 ![]() 是否需要挪走,并说明理由.
是否需要挪走,并说明理由.
参考答案:
【答案】
(1)解:如图,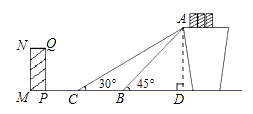
在Rt△ABD中,AD=ABsin45°![]() =4×
=4×![]() =2
=2![]() 在Rt△ACD中,
在Rt△ACD中,
∵∠ACD=30°,
∴AC=2AD=2×2![]() =4
=4![]() .
.
即新传送带AC的长度约为4![]() 米
米
(2)解:结论:货物MNQP不用挪走.解:在Rt△ABD中,BD=ABcos45°=4×![]() =2
=2![]() ,在Rt△ACD中,CD=
,在Rt△ACD中,CD= ![]() AD=2
AD=2![]() ×
×![]() =2
=2![]()
∴CB=CD-BD=2![]() -2
-2![]() ≈2.1
≈2.1
∵PC=PB-CB≈4-2.1=1.9<2,
∴货物MNQP不应挪走。
【解析】(1)在直角三角形中根据三角函数的定义,求出AD的长,根据在直角三角形中,30度角所对的边是斜边的一半,求出AC=2AD的值;(2)在直角三角形中,求出BD=AD的值,由三角函数的定义,得到CD的值,求出CB=CD-BD、PC=PB-CB的值,得到货物MNQP不应挪走.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的布口袋里装有白、红、黑三种颜色的小球,它们除了颜色之外没有其它区别,其中白球2只、红球1只、黑球1只. 袋中的球已经搅匀.
(1)随机地从袋中摸出1只球,则摸出白球的概率是多少?
(2)随机地从袋中摸出1只球,放回搅匀再摸出第二个球.请你用画树状图或列表的方法表示所有等可能的结果,并求两次都摸出白球的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,…,依次规律,第9个图形圆的个数为( )
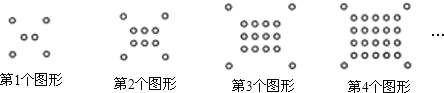
A.94B.85C.84D.76
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 是⊙
是⊙  的直径,
的直径,  是⊙
是⊙  上一点,∠
上一点,∠  的平分线交⊙
的平分线交⊙  于点
于点  ,交⊙
,交⊙  的切线
的切线  于点
于点  ,过点
,过点  作
作  ⊥
⊥  ,交
,交  的延长线于点
的延长线于点  .
.
(1)求证: 是⊙
是⊙  的切线;
的切线;
(2)若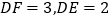 .求
.求 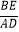 值.
值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,则∠AEB的度数为__________.
(2)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解方程组的部分过程,回答下列问题
解方程组

现有两位同学的解法如下:
解法一;由①,得x=2y+5,③
把③代入②,得3(2y+5)﹣2y=3.……
解法二:①﹣②,得﹣2x=2.……
(1)解法一使用的具体方法是________,解法二使用的具体方法是______,以上两种方法的共同点是________.
(2)请你任选一种解法,把完整的解题过程写出来
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )

A. 8
 B. 8 C. 4
B. 8 C. 4 D. 6
D. 6
相关试题

