【题目】(1)如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,则∠AEB的度数为__________.
(2)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.

参考答案:
【答案】(1)60°.(2)∠AEB=90°,AE=BE+2CM.理由见解析.
【解析】解:(1)∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=60°﹣∠DCB=∠BCE.
在△ACD和△BCE中,
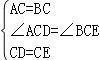 ,
,
∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°,
∴∠BEC=120°.
∴∠AEB=∠BEC﹣∠CED=60°.
(2)
∵△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°
∴CA=CB,CD=CE.
且∠ACD=∠BCE.
在△ACD和△BCE中,
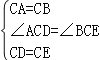 ,
,
∴△ACD≌△BCE(SAS).
∴AD=BE,∠ADC=∠BEC.
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°.
∵点A,D,E在同一直线上,
∴∠ADC=135°,
∴∠BEC=135°.
∴∠AEB=∠BEC﹣∠CED=90°.
∵CD=CE,CM⊥DE,
∴DM=ME.
∵∠DCE=90°,
∴DM=ME=CM.
∴AE=AD+DE=BE+2CM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答下列各题:
(1)x取何值时,代数式3x+2的值不大于代数式4x+3的值?(2)当m为何值时,关于x的方程
 x-1=m的解不小于3?
x-1=m的解不小于3? (3)已知不等式2(x+3)-4<0, 化简:︳4x+1︱-︱2-4x︱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=(x﹣2)2+3,当x 时,y随x的增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的是( )
A.对顶角相等B.同位角相等
C.内错角相等D.同旁内角互补
-
科目: 来源: 题型:
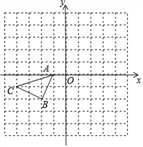
查看答案和解析>>【题目】如图,所示的边长为1的正方形网格中,△ABC 的顶点均在格点上,在所给平面直角坐标系中解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)作出将△ABC绕原点O按逆时针方向旋转90°后所得的△A2B2C2;
(3)写出点B1、B2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市今年中考数学学科开考时间是6月22日15时,数串“201506221500”中“0”出现的频数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】26个英文字母中,有很多都具有轴对称结构,请你写出其中具有轴对称结构的字母(至少3个) .
相关试题

